Rede neural convolucional
A rede neural convolucional (convolutional neural network - CNN) é um tipo de rede neural especializada no processamento e classificação de dados organizados em matrizes. Ela pode ser interpretada como uma rede MLP, modificada para trabalhar com dados bidimensionais. Seu nome deriva de uma operação semelhante à convolução, que é usada no lugar da simples multiplicação de matrizes em pelo menos uma de suas camadas.
Da mesma forma que a MLP, a CNN atualiza os pesos e biases por meio do algoritmo backpropagation. Ela é composta por camadas convolucionais para a extração de características, que servem como entrada para uma rede MLP totalmente conectada, responsável pela classificação. As camadas convolucionais também possuem estágios com operações de subamostragem, conhecidas como agrupamento (pooling). A subamostragem reduz a resolução do mapa de características e diminui a sensibilidade da saída a translações e outras formas de distorção.
A seguir, vamos detalhar essa rede.
Convolução e camadas convolucionais
Seja \(w(n)\) a resposta impulsiva de um filtro de tempo discreto. A relação entrada-saída desse filtro é dada pela operação de convolução entre a sequência de entrada \(x(n)\) e sua resposta impulsiva \(w(n)\), ou seja, \[ y(n)=x(n)\ast w(n)=\sum_{k=-\infty}^{\infty}x(k)w(n-k)=\sum_{k=-\infty}^{\infty}w(k)x(n-k) \]
para qualquer inteiro \(n\). A última igualdade vem do fato da convolução ser comutativa. Se o filtro for causal e com resposta impulsiva finita (FIR – finite impulse response) com \(M\) coeficientes, \(\{w(n)\}_{n=0}^{M-1}\), e a sequência de entrada tiver \(N\) amostras, \(\{x(n)\}_{n=0}^{N-1}\), o resultado da convolução se reduz a \[ y(n)=\sum_{k=0}^{M-1}w(k)x(n-k). \]
Neste caso, a sequência de saída \(y(n)\) terá \(N+M-1\) amostras.
No caso bidimensional, a convolução entre uma imagem \(\mathbf{I}(i,j)\) e um filtro \(\mathbf{K}(i,j)\) é dada por \[ \mathbf{S}(i,j)=\mathbf{I}(i,j)\ast \mathbf{K}(i,j)=\sum_{m}\sum_{n}\mathbf{I}(m,n)\mathbf{K}(i-m,j-n). \]
Novamente, devido à propriedade comutativa, podemos escrever \[ \mathbf{S}(i,j)=\mathbf{K}(i,j)\ast \mathbf{I}(i,j)=\sum_{m}\sum_{n}\mathbf{I}(i-m,j-n)\mathbf{K}(m,n). \]
Em aprendizado de máquina, é comum considerar a correlação cruzada no lugar da convolução, o que leva a \[ \mathbf{S}(i,j)=\mathbf{K}(i,j)\star \mathbf{I}(i,j)=\sum_{m}\sum_{n}\mathbf{I}(i+m,j+n)\mathbf{K}(m,n), \]
em que usamos o símbolo \(\star\) em vez do símbolo \(\ast\) para indicar essa operação. Esse cálculo é semelhante ao da convolução, a menos do fato de que não se considera o rebatimento da entrada (ou do filtro).
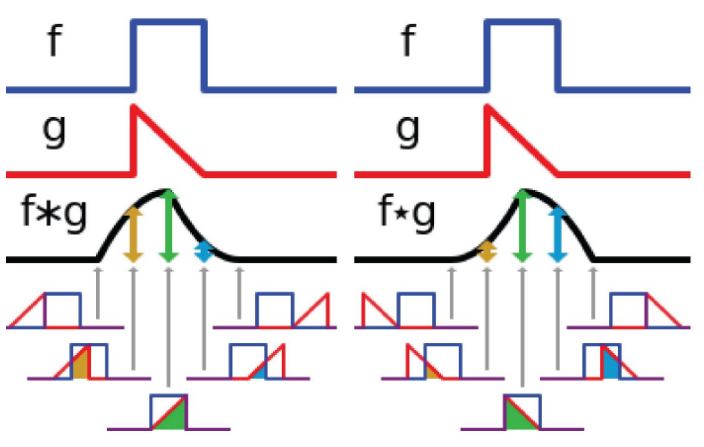
Na Figura 1, é mostrado um exemplo de cálculo da convolução e da correlação cruzada para uma dimensão, considerando duas funções de tempo contínuo \(f\) e \(g\). Muitas bibliotecas de aprendizado de máquina implementam a correlação cruzada e chamam essa operação de convolução sem rebatimento ou simplesmente de convolução. Diante disso, também vamos chamar essa operação aqui de convolução.
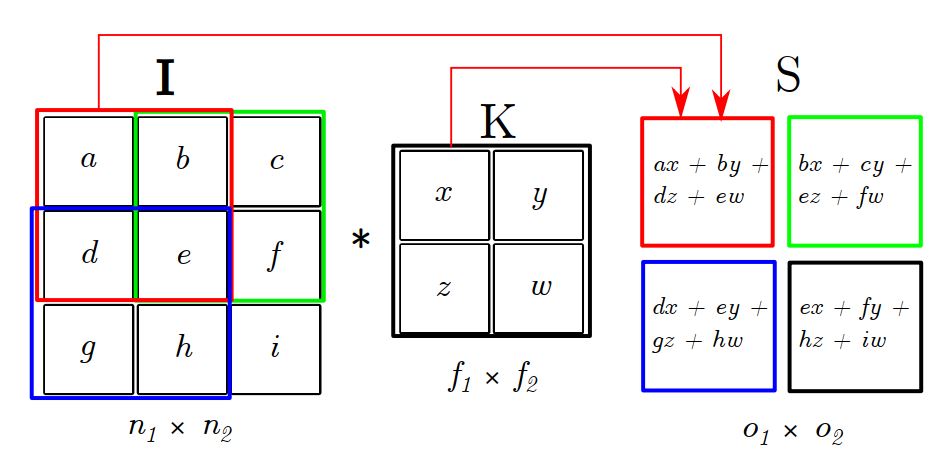
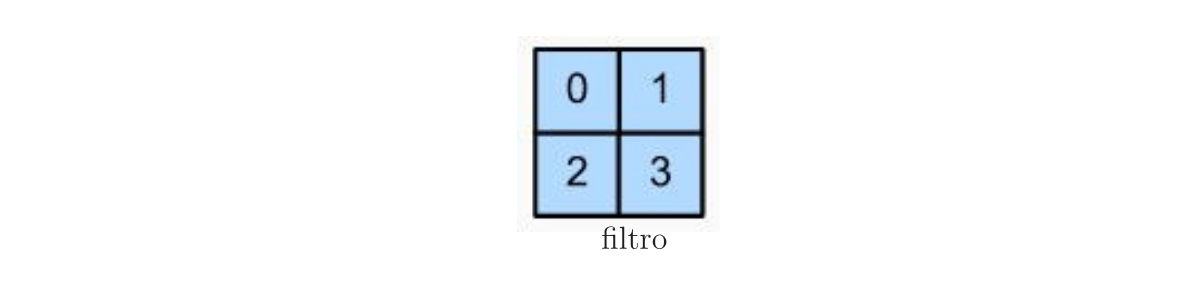
Na Figura 2, é exemplificada a convolução da imagem \(\mathbf{I}\) de dimensões \((n_1 \times n_2)=(3\times 3)\) com o filtro \(\mathbf{K}\) de dimensões \((f_1 \times f_2)=(2\times 2)\), que gera a saída \(\mathbf{S}\) de dimensões \((o_1 \times o_2)=(2\times 2)\). De forma geral, as dimensões de \(\mathbf{S}\) são iguais a \[ (o_1 \times o_2) = (n_1-f_1+1\;\times\; n_2-f_2+1). \]
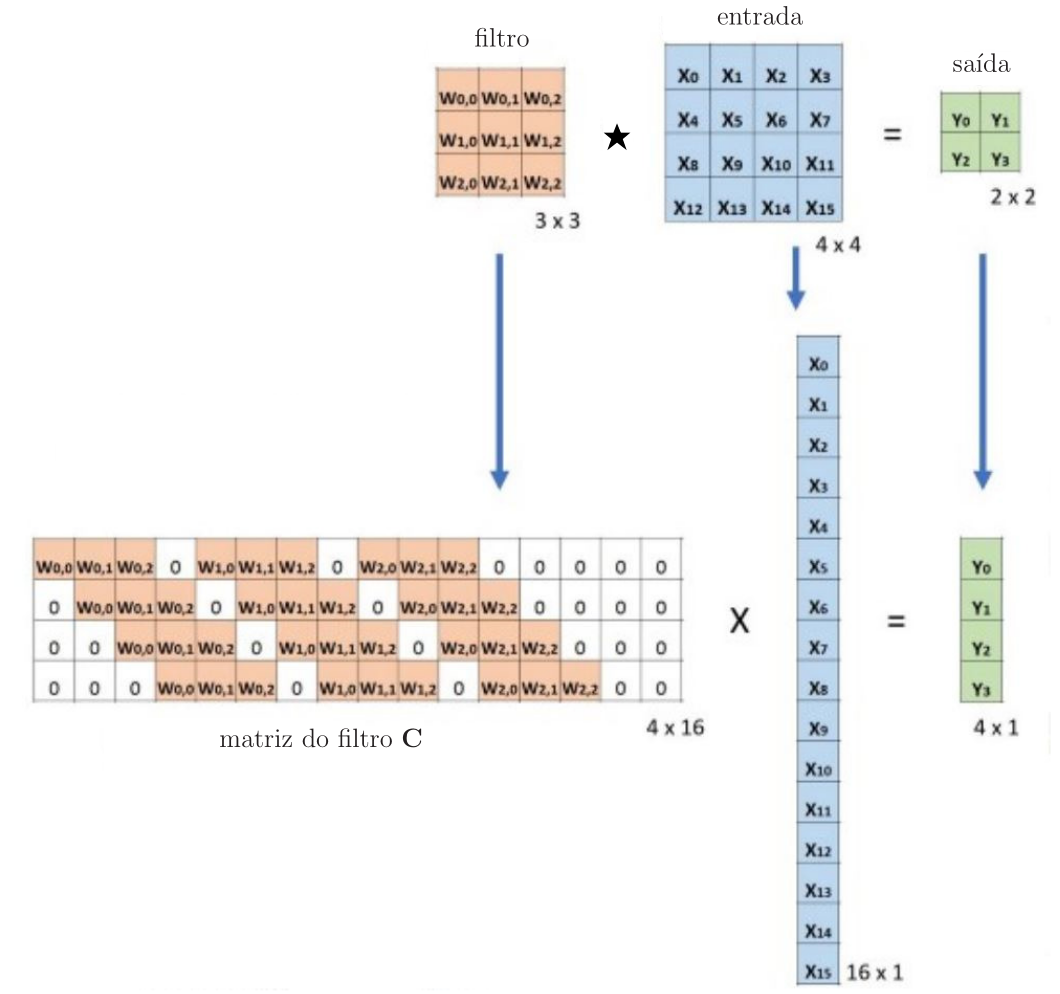
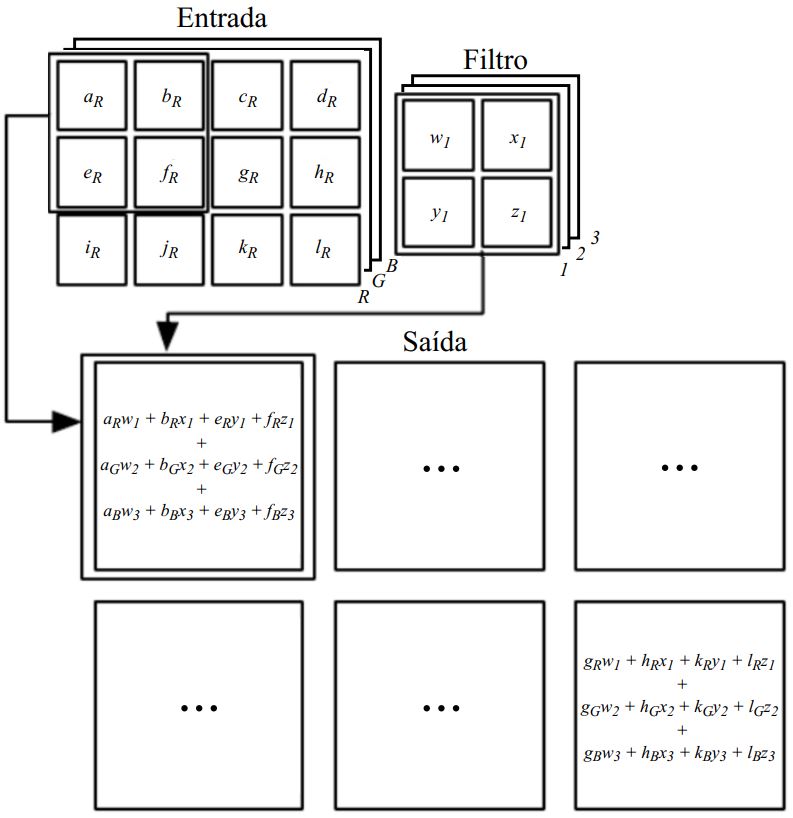
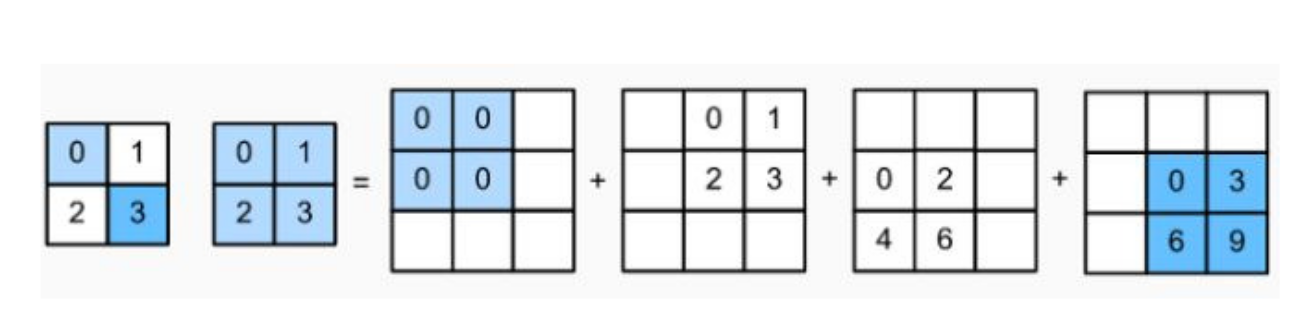
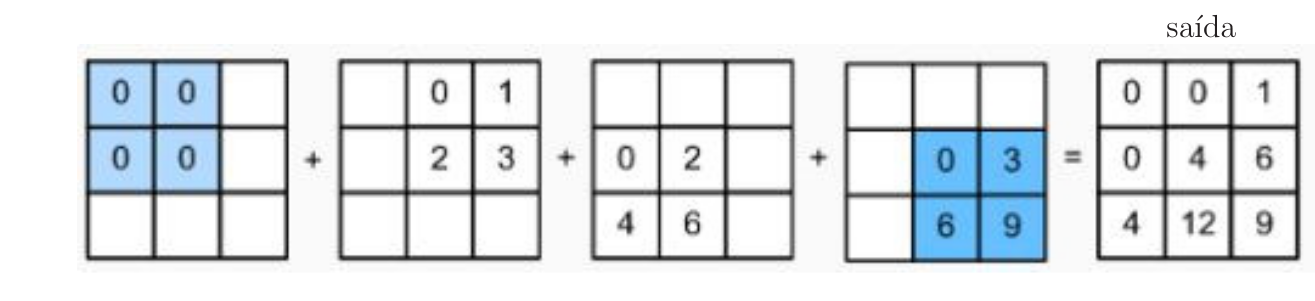
A convolução pode ser implementada por meio da multiplicação de matrizes. Para isso, vamos definir a matriz de convolução do filtro denotada por \(\mathbf{C}\), como ilustrado na Figura 3. A convolução de uma entrada \(4\times 4\) com um filtro \(3\times 3\) leva à saída \(2\times 2\). Essa convolução pode ser implementada pela multiplicação da matriz de convolução \(\mathbf{C}\) de dimensões \(4\times 16\) pelo vetor \(16\times 1\), o que leva ao vetor de saída \(4\times 1\). Na sequência, o vetor resultante \(4\times 1\) deve então ser transformado de volta para uma saída \(2\times 2\).
Em cada estágio de convolução de uma camada convolucional, é comum considerar \(k\) filtros, com \(k\geq 1\). Para cada filtro, calcula-se a convolução entre a entrada e o filtro e a esse resultado soma-se o bias. Os elementos da matriz resultante entram em uma função de ativação não linear e uma das matrizes da saída é obtida. A saída terá uma dimensão a mais, igual ao número de filtros da camada (\(k\)). É comum considerar filtros quadrados (\(f_1=f_2=f\)) e de mesmo tamanho para uma dada camada. A consequência é que as dimensões da saída de uma camada convolucional serão dadas por
\[ (n_1-f+1)\times(n_2-f+1)\times k. \]
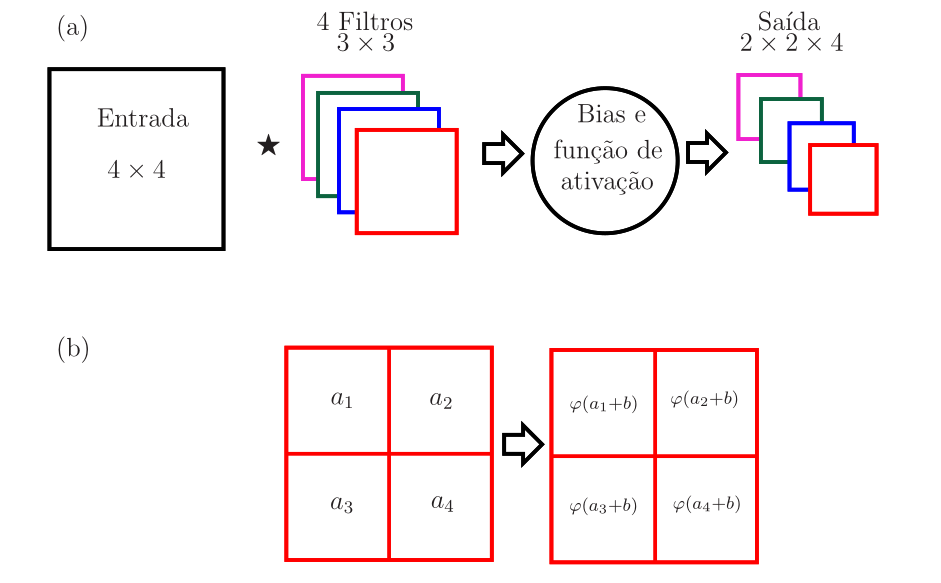
Na Figura 4-(a), esse processo é ilustrado considerando uma entrada de dimensões \(4 \times 4\) e uma camada convolucional com quatro filtros de dimensões \(3\times 3\), o que gera a saída de dimensões \(2\times 2\times 4\). Na Figura 4-(b), a soma do bias e a aplicação da função de ativação são ilustradas para uma das matrizes resultantes da convolução. Os filtros das camadas convolucionais são matrizes de pesos. Assim, considerando os quatro filtros de dimensões \(3\times 3\) da Figura 4-(a), há \(4 \times 3 \times 3 = 36\) pesos e \(4\) biases (um bias por filtro).
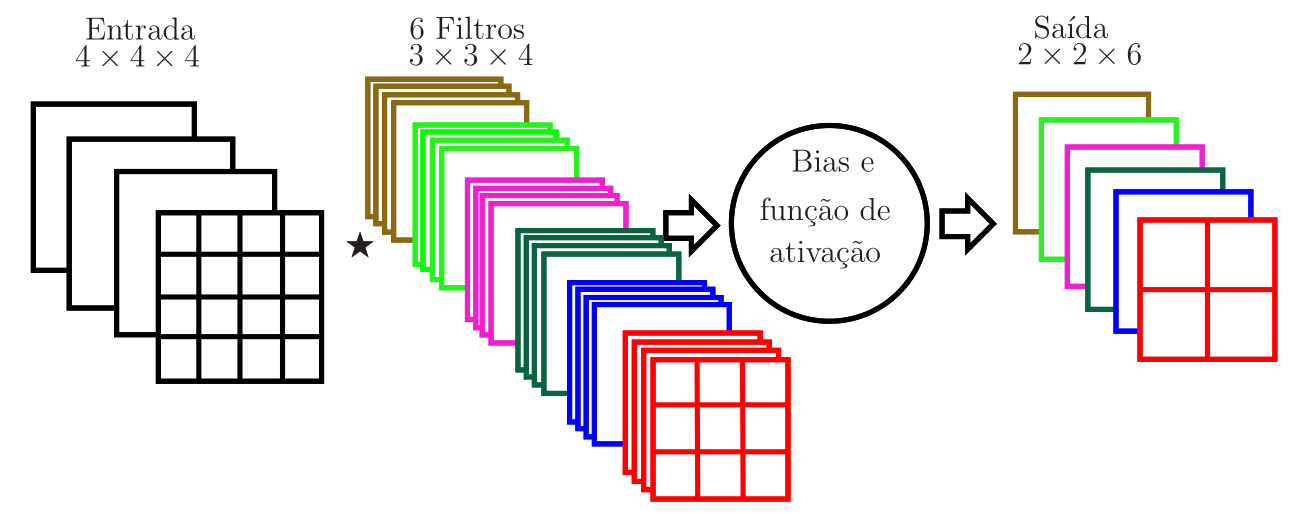
Caso a entrada de um estágio de convolução da camada convolucional seja um tensor, como a saída de dimensões \(2\times 2 \times 4\) da Figura 4, os filtros dessa camada devem ter sua terceira dimensão igual à terceira dimensão da entrada, denotada por \(n_3\). Neste caso, a convolução deve levar em conta as \(n_3\) matrizes que compõem o tensor de entrada e as \(n_3\) matrizes que compõem cada filtro, como ilustrado na Figura 5 para \(n_3=3\). No exemplo dessa figura, note que a entrada tem dimensões \((4\times 4 \times 3)\), há apenas um filtro de dimensões \((2\times 2\times 3)\), o que leva à saída da convolução com dimensões \((3\times 3 \times 1)\). Para uma entrada de dimensões \(n_1\times n_2\times n_3\) e \(k\) filtros de dimensões \(f\times f\times n_3\), a saída terá dimensões \((n_1-f+1)\times (n_2-f+1) \times k\). Na Figura 6, é ilustrado um estágio de convolução com entrada de dimensões \((4 \times 4 \times 4)\) e seis filtros de dimensões \((3\times 3 \times 4)\), que levam à saída de dimensões \((2\times 2\times 6)\). Há \(6\times 3 \times 3 \times 4 =216\) pesos e \(6\) biases nesta camada.
Zero padding e stride
Ao se calcular a convolução da entrada \(\mathbf{I}\) com o filtro \(\mathbf{K}\), a matriz de saída \(\mathbf{S}\) fica com dimensões menores que as da entrada. Se houver uma cascata de filtros, as dimensões da matriz de saída de cada filtro vão diminuindo ao longo da cascata. Isso faz com a matriz de saída se torne quase sem sentido depois de várias convoluções devido às suas dimensões muito reduzidas. Além disso, pode-se perder informações valiosas ao se descartar completamente as bordas da entrada.
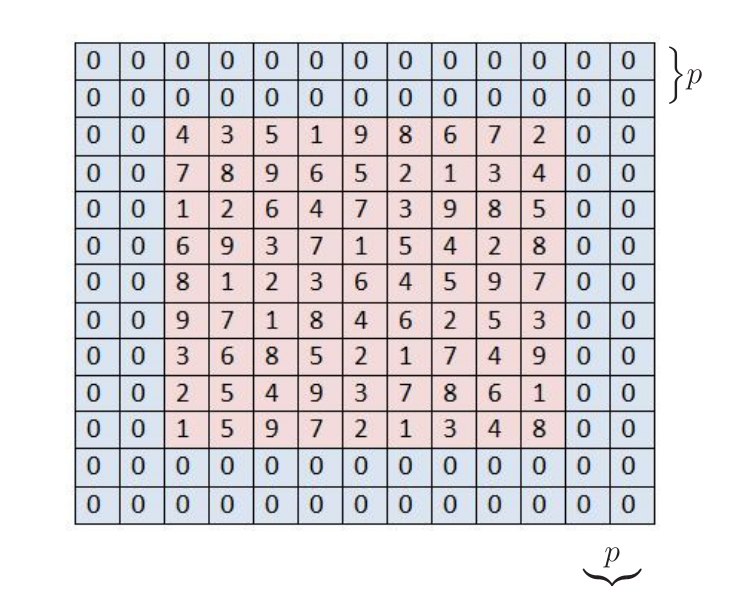
Para que a matriz \(\mathbf{S}\) fique com as mesmas dimensões da entrada \(\mathbf{I}\), adicionam-se bordas preenchidas com zeros à matriz \(\mathbf{I}\). Essa prática é conhecida como zero padding. Para exemplificar, considere a matriz de entrada \(\mathbf{I}\) com dimensões \((n_1 \times n_2)=(9\times 9)\) indicada no quadrado vermelho da Figura 7. Preenchendo a matriz \(\mathbf{I}\) com \(p\) bordas de zeros, suas dimensões se tornam iguais a
\[ (n_1+2p\times n_2+2p). \]
No exemplo da Figura 7, \(p=2\) e as dimensões de \(\mathbf{I}\) ficam \((n_1+2p\times n_2+2p)=(13\times 13)\). As dimensões da matriz \(\mathbf{S}\), por sua vez, ficam iguais a
\[ (o_1 \times o_2) = (n_1+2p-f_1+1 \;\times\; n_2+2p-f_2+1). \]
Para que as dimensões da saída sejam as mesmas da entrada, deve-se considerar
\[ p=\frac{f_1-1}{2}=\frac{f_2-1}{2}. \]
Dessa forma, conclui-se que para manter as dimensões da saída iguais às da entrada, o filtro deve ser quadrado, ou seja \(f_1=f_2=f\), o que leva a \(p=({f-1})/{2}\). Note que para que \(p\) seja inteiro, \(f\) deve ser ímpar. Se \(f\) for par, uma possibilidade é adicionar \(\lceil (f-1)/2 \rceil\) linhas de zeros no topo e \(\lfloor (f-1)/2 \rfloor\) linhas de zeros na parte inferior da matriz \(\mathbf{I}\). Devemos fazer o mesmo para as colunas à esquerda e à direita. Geralmente, os filtros usados nas CNNs têm dimensões ímpares, o que facilita o zero padding. Apesar da entrada na Figura 7 ser quadrada, não existe restrições para as dimensões dessa matriz, ou seja, podemos ter \(n_1\neq n_2\).
No cálculo da convolução, começamos com a janela do filtro no canto superior esquerdo da matriz de entrada e deslocamos essa janela para baixo e para a direita. No exemplo da Figura 2, deslocamos uma linha ou coluna por vez. No entanto, podemos deslocar o filtro sobre a matriz de entrada mais de uma linha ou coluna por vez. Isso é vantajoso em termos computacionais e reduz a resolução, o que é desejável em alguns casos. Esse método é conhecido como stride. A quantidade de linhas ou colunas percorridas de uma só vez pelo filtro é denotada por \(s\). Ao considerar zero padding \(p\) e stride \(s\), as dimensões da matriz \(\mathbf{S}\) ficam iguais a
\[ (o_1 \times o_2) = \left(\left\lfloor \frac{n_1+2p-f_1}{s}+1\right\rfloor \;\times\; \left\lfloor \frac{n_2+2p-f_2}{s}+1\right\rfloor \right). \]
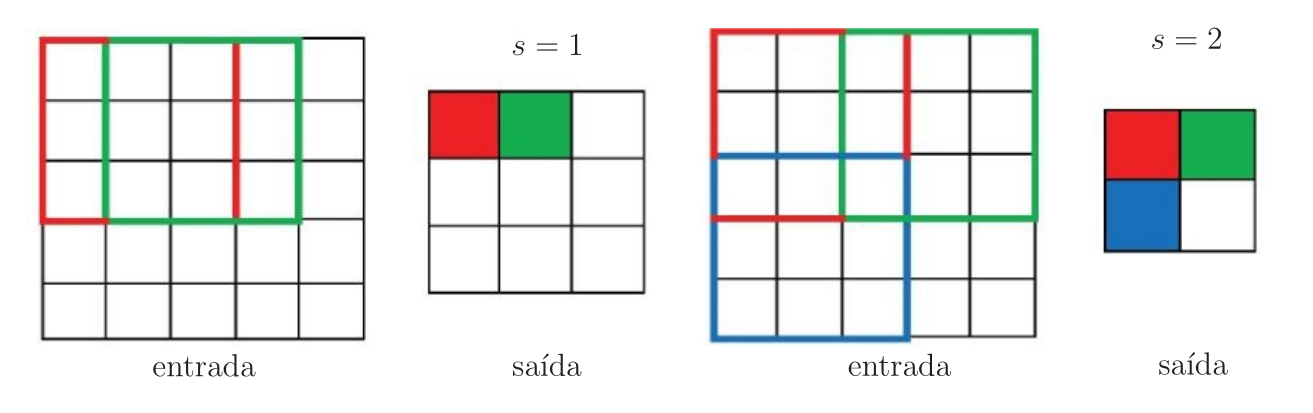
Na Figura 8, é mostrado um exemplo de convolução com stride e sem zero padding (\(p=0\)), considerando \(s=1\) e \(s=2\). Neste exemplo, a matriz de entrada \(\mathbf{I}\) tem dimensões \((n_1 \times n_2)=(5\times 5)\) e o filtro \(\mathbf{K}\) tem dimensões \((f_1 \times f_2)=(3\times 3)\). O resultado com \(s=1\) é uma matriz de saída com dimensões \((o_1 \times o_2)=(3\times 3)\). Já com \(s=2\), a matriz de saída passa a ter dimensões \((o_1 \times o_2)=(2\times 2)\).
Pooling
As camadas convolucionais são os blocos básicos de uma CNN. Uma camada convolucional desloca um filtro sobre a imagem e extrai características, resultando em um mapa de características. Esse mapa de características, por sua vez, pode ser alimentado para a próxima camada convolucional para extrair características em um nível superior e assim sucessivamente. Empilhar várias camadas convolucionais permite que uma CNN reconheça estruturas e objetos cada vez mais complexos em uma imagem.
Um problema que surge é que o mapa de características produzido pelo filtro é dependente da localização. Isso significa que durante o treinamento, a CNN aprende a associar a presença de uma determinada característica a um local específico na imagem de entrada, o que pode prejudicar seu desempenho. Em vez disso, deseja-se que o mapa de características e a rede sejam invariantes à translação para que a localização da característica deixe de importar.
Uma das técnicas usadas para tornar as CNNs invariantes à translação é o agrupamento (pooling), também chamado de subamostragem. Existem diferentes abordagens para o agrupamento, sendo o agrupamento máximo (max-pooling) e o agrupamento médio (average pooling) os mais utilizados. Além de tornar as CNNs invariantes à translação, o pooling reduz as dimensões das matrizes. Na Figura 9, é mostrado um exemplo numérico de pooling, considerando (a) max-pooling e (b) average pooling. Uma imagem de dimensões \(6\times 6\) foi transformada em uma imagem \(3\times 3\). No caso do max-pooling (Figura 9-(a)), os quatro pixels da região azul foram substituídos pelo valor máximo, \(9\) no caso. O mesmo aconteceu com os pixels da região laranja, que foram substituídos pelo valor \(7\). No caso do average pooling (Figura 9-(b)), a média dos pixels da região azul dá 4,5, que arredondando leva ao valor \(5\). Já a média dos pixels da região laranja dá \(4\).
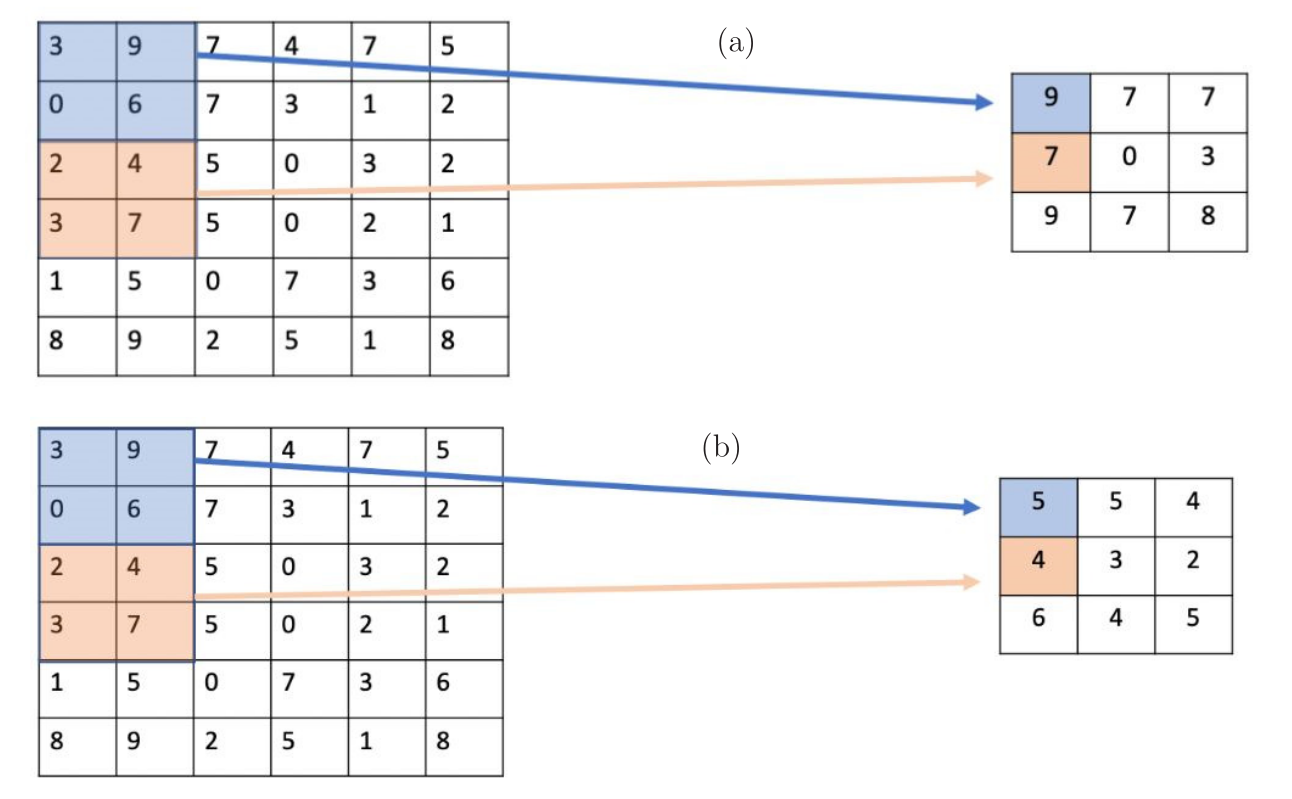
Se a rede neural dependesse apenas do mapa de características original, sua capacidade de detectar uma característica dependeria da localização no mapa. Por exemplo, se o valor \(9\) fosse encontrado apenas no quadrante superior esquerdo, a rede aprenderia a associar a característica relativa ao número 9 com o quadrante superior esquerdo. Ao aplicar o agrupamento, essa característica é extraída em um mapa menor e mais geral que indica apenas se uma característica está presente naquele quadrante específico ou não. A cada camada adicional, o mapa se torna menor, preservando apenas as informações importantes sobre a presença das características de interesse. À medida que o mapa se torna menor, torna-se cada vez mais independente da localização da característica. O pooling é especialmente útil para classificação de imagem em que se deseja detectar a presença de um determinado objeto em uma imagem, mas não se importa onde exatamente ele está localizado.
Convolução transposta
Em algumas aplicações, deseja-se fazer transformações que vão na direção oposta de uma convolução tradicional, ou seja, deseja-se realizar uma sobreamostragem. Este é o caso, por exemplo, de redes usadas para geração de imagens de alta resolução e redes usadas para extração de características por meio de autoencoders.
Tradicionalmente, a sobreamostragem é obtida aplicando-se esquemas de interpolação ou criando regras manualmente. No entanto, as redes neurais podem aprender a transformação adequada automaticamente por meio da convolução transposta. Essa operação também é chamada na literatura de desconvolução. No entanto, esse termo não é adequado uma vez que desconvolução em processamento de sinais é a operação inversa da convolução, cujo objetivo é desfazer a convolução, ou seja obter a imagem original a partir de uma imagem que é fruto da convolução da original com um filtro.
É possível implementar uma convolução transposta utilizando a convolução. Para exemplificar, é mostrado na Figura 10 uma convolução transposta considerando um filtro \(3\times 3\) sobre uma entrada \(2\times 2\) modificada com zero padding de \(p=2\) e stride de passo unitário, \(s=1\). A saída sobreamostrada tem dimensões \(4 \times 4\). Neste caso, as dimensões da saída são maiores que as da entrada devido ao zero padding. Cabe observar que a convolução transposta gera o mesmo resultado da convolução tradicional ao considerarmos a entrada aumentada com zeros. Pode-se mapear a mesma imagem de dimensões \(2\times 2\) em uma imagem de dimensões ainda maiores, aplicando um zero padding mais sofisticado. Na Figura 11, a convolução transposta é aplicada sobre a mesma entrada \(2\times 2\) com \(p=2\) e \(s=1\), além de um zero inserido entre os pixels. Neste caso, a saída fica com dimensões \(5 \times 5\).
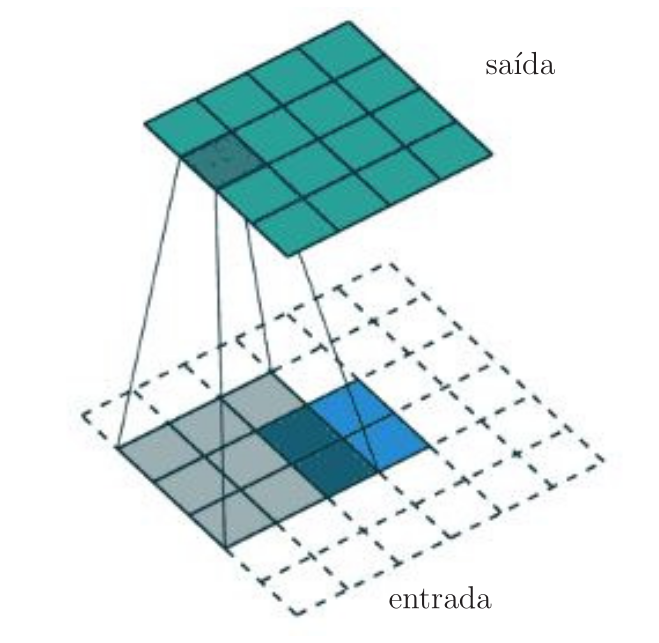
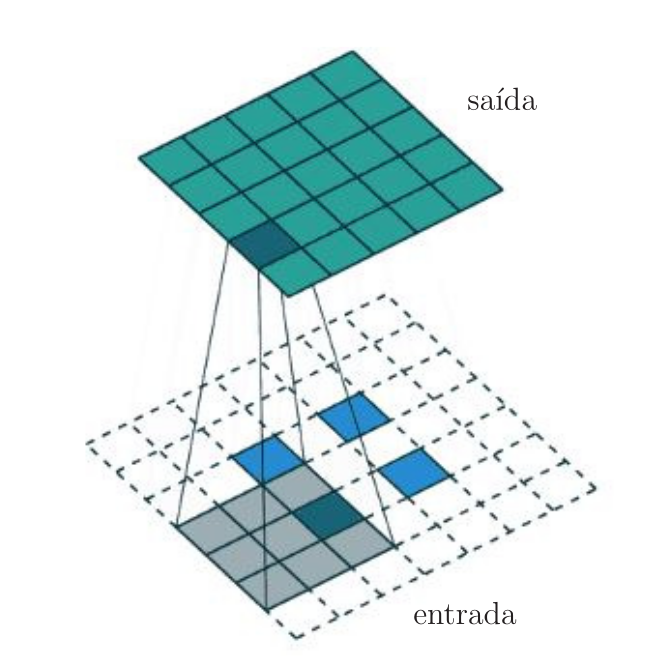
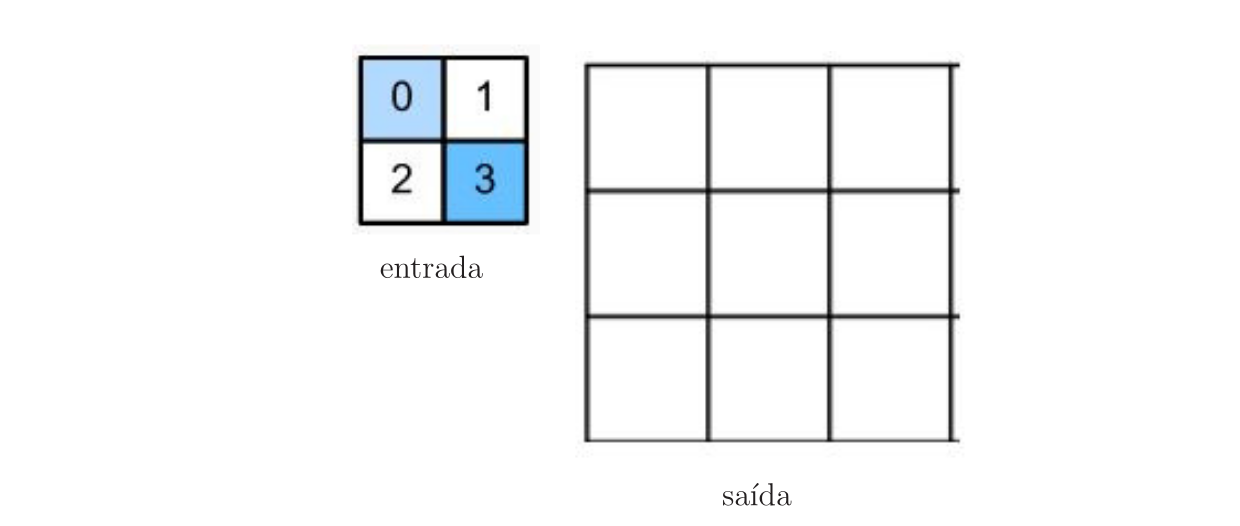
Outra forma de implementar a convolução transposta é seguindo os passos exemplificados a seguir [Fonte]:
- Considere um mapa de características \(2\times 2\) que precisa ser sobreamostrado para um mapa de características \(3\times 3\).
- Considere o filtro \(2\times 2\)
- Multiplique o elemento superior esquerdo do mapa de características de entrada por cada elemento do filtro:

- Repita o Item 3 para cada elemento do mapa de características de entrada:
- Alguns dos elementos dos mapas de características resultantes da sobreamostragem ficam sobrepostos. Para resolver esse problema, os elementos das posições sobrepostas devem ser adicionados. Assim, obtém-se a saída final.
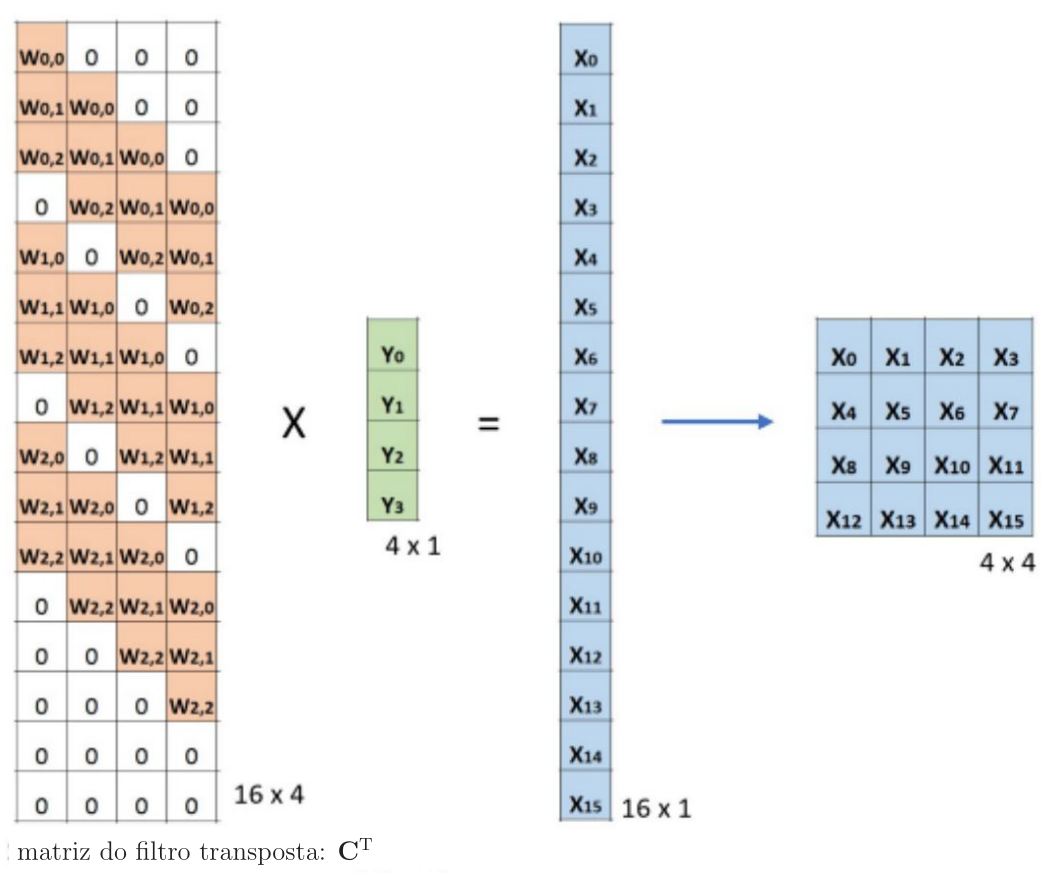
Para finalizar, considere a implementação da convolução por meio da multiplicação de matrizes, exemplificada na Figura 3. Multiplicando a matriz do filtro transposta de dimensões \(16\times 4\) pelo vetor de entrada \(4\times 1\), que inclusive pode ser a saída vetorizada de uma camada convolucional anterior, obtém-se um vetor de dimensões \(16\times 1\). Comparando com a entrada que continha apenas 4 pixels, esse procedimento levou a uma saída aumentada com dimensões \(4\times 4\), como mostrado na Figura 12. Não podemos esquecer que os pesos devem ser atualizados para que a sobreamostragem se adéque à aplicação. O fato de usarmos a matriz do filtro transposta \(\mathbf{C}^{\rm T}\) justifica o nome dessa operação.
Estrutura de uma CNN
Depois de aprendermos como é feita a convolução nas camadas convolucionais em conjunto com os métodos de zero padding (preenchimento com zeros), stride (passo largo) e pooling (subamostragem), podemos agora analisar a estrutura completa de uma CNN típica, como ilustrado na Figura 13. Uma CNN típica é composta de camadas convolucionais para extração de características, seguida de uma MLP totalmente conectada para classificação. Suponha que se deseja identificar se a imagem de entrada da rede corresponde ao Pato Donald, ao Pateta (Goofy) ou ao Piu-Piu (Tweety). Nas camadas convolucionais é comum alternar estágios de convolução e subamostragem (pooling). Como vimos, a subamostragem é importante para que o mapa de características se torne invariante à translação. O mapa de características subamostrado da última camada convolucional deve ser vetorizado. Em seguida, esse vetor entra na MLP. No exemplo da Figura 13, a MLP é composta de uma camada oculta e uma camada de saída. No entanto, em muitos problemas é comum considerar uma MLP profunda, com várias camadas ocultas. Para classificação multiclasse, considera-se a entropia cruzada como função custo e a função de ativação softmax, que fornece a probabilidade da classificação. No caso da Figura 13, há três neurônios de saída e com os valores obtidos pela softmax que estão indicados na figura, decide-se que a imagem é do Piu-Piu.
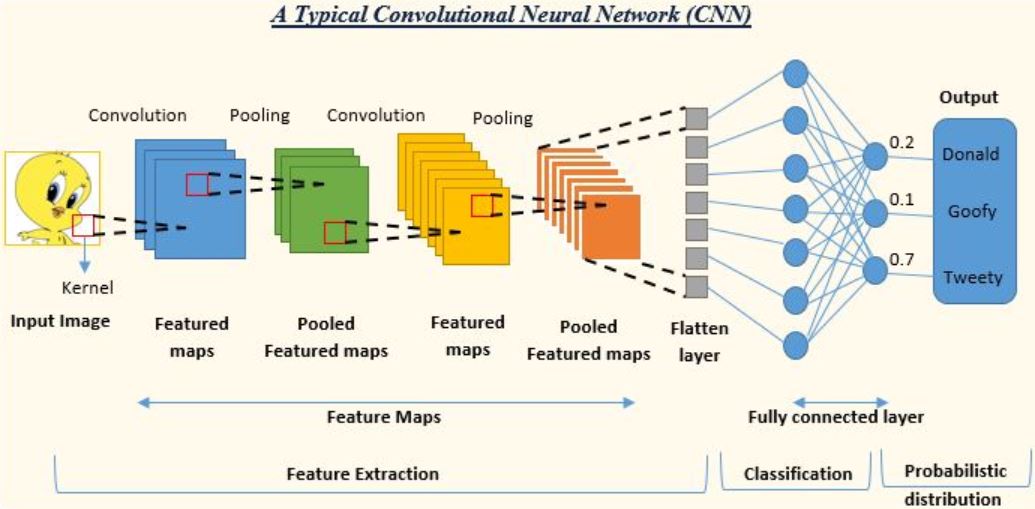
Os pesos dos filtros das camadas convolucionais e dos neurônios da MLP são atualizados com o algoritmo backpropagation
Exemplo de aplicação
Esse exemplo foi explorado em https://atcold.github.io/pytorch-Deep-Learning/en/week03/03-3/. Nesse exemplo, uma rede MLP e uma CNN foram treinadas para classificação do conjunto de dados MNIST, disponível em http://yann.lecun.com/exdb/mnist/. Trata-se de um banco de dados de dígitos manuscritos, que possui um conjunto de treinamento de 60000 exemplos e um conjunto de teste de 10000 exemplos.
As redes MLP e CNN treinadas têm o mesmo número de parâmetros. Na Figura 14, são mostrados exemplos de treinamento do banco de dados MNIST original. Antes do treinamento, os dados foram normalizados para que a inicialização da rede corresponda à distribuição de dados. Além disso, as cinco etapas foram usadas no treinamento:
- Alimentação dos dados no modelo;
- Cálculo da função custo;
- Limpeza do cache de gradientes acumulados;
- Cálculo dos gradientes;
- Execução do método de otimização.
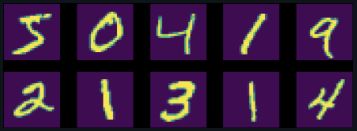
Primeiramente, ambas as redes foram treinadas com os dados MNIST normalizados. A MLP atingiu uma acurácia de 87% enquanto a acurácia da CNN ficou igual a 95%. Dado o mesmo número de parâmetros, a CNN conseguiu treinar muito mais filtros. Na rede MLP, os neurônios tentam obter algumas dependências entre pixels mais distantes com pixels próximos, o que acaba sendo desperdiçado. Em vez disso, na CNN, os parâmetros se concentram no relacionamento entre os pixels vizinhos.
Em seguida, foi feita uma permutação aleatória de todos os pixels em todas as imagens do conjunto de dados MNIST. Isso transforma a Figura 14 na Figura 15. Ambas as redes foram treinadas com esse conjunto de dados modificado.

O desempenho da rede MLP quase se manteve inalterado (85%), mas a acurácia da CNN caiu para 83%. Isso ocorre porque, após uma permutação aleatória, as imagens não possuem mais as três propriedades de localidade, estacionariedade e composicionalidade, que são exploradas por uma CNN.