A rede perceptron multicamada
Apesar do perceptron de Rosenblatt ter sido proposto no final da década de 1950, o algoritmo de retropropagação (backpropagation), utilizado no treinamento das redes neurais, surgiu apenas em 1986 no artigo (Rumelhart, Hinton, e Williams 1986). Desde então, ele tem sido abordado em diferentes livros de redes neurais e aprendizado de máquina como, por exemplo, (Haykin 2009), (Bishop 2006), (Goodfellow, Bengio, e Courville 2016), (Theodoridis e Koutroubas 2003), (Witten et al. 2017), (Izenman 2008), (Duda, Hart, e Stork 2001), (Kinsley e Kukiela 2020), (Kröse e Smagt 1996), entre muitos outros. A seguir, vamos tratar da rede percepton multicamada (multilayer perceptron - MLP) e do algoritmo backpropagation em detalhes.
O modelo da rede e o cálculo progressivo
O modelo do neurônio proposto por Rosenblatt é usado até hoje nas redes neurais. A diferença está apenas na função não linear, chamada de função de ativação. No modelo de Rosenblatt, utilizou-se a função sinal que tem derivada nula em todos os pontos, exceto na origem onde não é definida. Em vez dessa função, é comum utilizar funções de ativação com derivada não nula e definida em todos os pontos, como a função sigmoidal, a tangente hiperbólica, entre outras. Essas funções permitem chegar ao algoritmo de retropropagação (backpropagation) como veremos mais adiante.
Considerando o \(n\)-ésimo vetor dos dados de treinamento
\[ \mathbf{x}(n)=[\,1\;x_{1n}\; x_{2n}\; \cdots\; x_{Mn}\,]^{\rm T} \]
e o vetor de pesos e bias com dimensão \(M+1\)
\[ \mathbf{w}(n) = [\,b(n)\;w_1(n)\;\cdots\;w_M(n)\,]^{\rm T}, \]
a saída do combinador linear pode ser escrita como
\[ v(n) = \mathbf{x}^{\rm T}(n)\mathbf{w}(n-1) \]
e a saída do neurônio é dada por
\[ y(n)=\varphi(v(n)), \]
em que \(\varphi(\cdot)\) é a função de ativação. Cabe observar que nesta formulação, o bias aparece na primeira posição do vetor \(\mathbf{w}\) e por isso, o vetor de entrada \(\mathbf{x}\) tem sempre o valor \(1\) em sua primeira posição. O diagrama de fluxo de sinal do neurônio está mostrado na Figura 1.
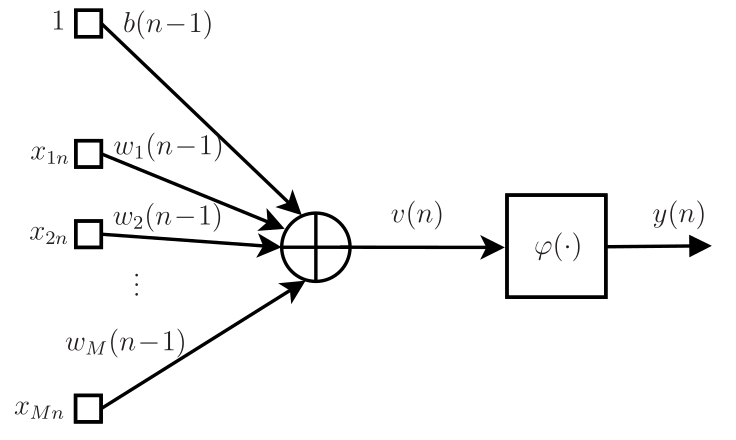
O neurônio da Figura 1 é a unidade básica da rede perceptron multicamada (multilayer perceptron - MLP). Na maior parte das aplicações, um único neurônio não é suficiente para se obter bons resultados. Dessa forma, a rede MLP organiza os neurônios em camadas, havendo uma ou mais camadas ocultas (hidden layers) e a camada de saída1. As camadas ocultas são camadas intermediárias entre a entrada e a saída da rede neural. Cada neurônio pertencente a uma camada oculta possui sinapses associadas a pesos, ligando-o a todos os neurônios da camada anterior. No caso da primeira camada oculta, em cada neurônio, as \(N_0\triangleq M\) entradas da rede são ponderadas pelos pesos, que junto com o bias, permitem o cálculo da combinação linear, representada na Figura 1 por \(v(n)\). Na Figura 2, esquematizamos o fluxo de sinal de uma rede MLP com \(L=3\) camadas, em que cada círculo representa um neurônio. Denotando o número de neurônios da camada \(j\) por \(N_{j}\), é conveniente introduzir uma notação para a configuração da rede. Assim, uma rede MLP de 3 camadas apresenta configuração \(N_0\)-\(N_1(\varphi_1)\)-\(N_2(\varphi_2)\)-\(N_3(\varphi_3)\). Apesar de ser possível utilizar diferentes funções de ativação em uma mesma camada, é comum considerar a mesma função para todos os neurônios de uma dada camada, o que é contemplado pela notação que acabamos de introduzir. Especificamente, a rede da Figura 2 tem configuração \(3\)-\(3(\text{tanh})\)-\(2(\text{tanh})\)-\(2(\text{sgm})\), ou seja, \(N_0=3\) entradas, \(N_1=3\) neurônios na primeira camada oculta, \(N_2=2\) neurônios na segunda camada oculta e \(N_3=2\) neurônios na camada de saída. Os neurônios das camadas ocultas têm como função de ativação a tangente hiperbólica (tanh) e os de saída, a função sigmoidal (sgm), ou seja, \(\varphi_1=\varphi_2=\text{tanh}\) e \(\varphi_3=\text{sgm}\). Também vamos denotar o número de neurônios da camada de saída por \(N_L\). Assim, no exemplo, \(N_L=N_3=2\).
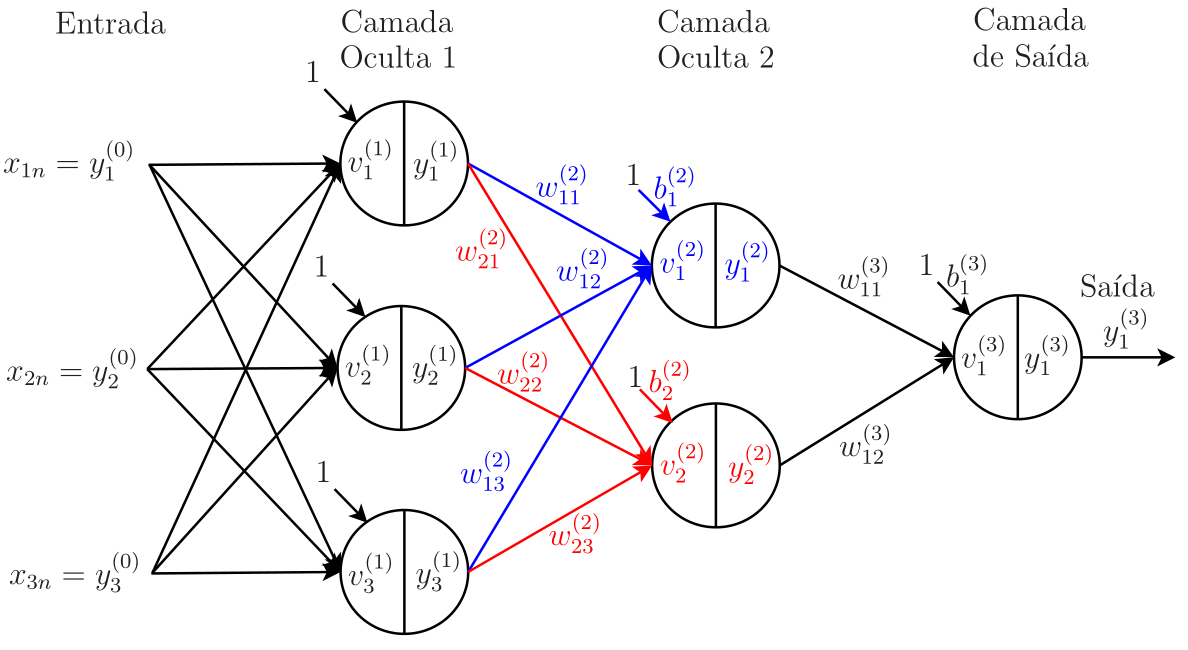
Vamos usar o exemplo da rede MLP da Figura 2 para calcular a saída da camada oculta 2, cujos pesos estão indicados. É importante atentar para a notação: \(\omega_{k\ell}^{(j)}\) representa o peso que liga o neurônio \(\ell\) da camada \(j-1\) ao neurônio \(k\) da camada \(j\). Se o neurônio \(k\) pertencer à primeira camada oculta, devemos trocar “neurônio \(\ell\)” na frase anterior por “entrada \(\ell\)”. Voltando à Figura 2, observe que a entrada da rede é dada pelo vetor
\[ [x_{1n}\;\; x_{2n}\;\;\cdots\;\; x_{N_0n}]^{\rm T}, \]
que corresponde ao \(n\)-ésimo dado do conjunto de treinamento, em que \(N_0\) é o número de entradas (\(N_0=3\) no exemplo). É conveniente usar a notação \(y_k^{(0)}\triangleq x_{kn}\), \(k=1,2,\ldots, N_0\) para denotar os elementos do vetor de entrada. Dessa forma, podemos definir o vetor de entrada da rede como
\[ \mathbf{y}^{(0)} \triangleq \begin{bmatrix} y^{(0)}_1 \\ y^{(0)}_2 \\ \vdots \\ y^{(0)}_{N_0} \end{bmatrix}. \]
Para simplificar a notação, o índice \(n\) relacionado ao \(n\)-ésimo dado de treinamento não será levado em conta nesta seção. Em cada neurônio da primeira camada oculta, esse vetor é ponderado e somado ao bias. A saída de cada neurônio é então calculada aplicando-se a função de ativação \(\varphi_1(\cdot)\) ao resultado dessa combinação linear. Reunindo as saídas dos neurônios da primeira camada oculta em um vetor, temos
\[ \mathbf{y}^{(1)} = \begin{bmatrix} y^{(1)}_1 \\ y^{(1)}_2 \\ \vdots \\ y^{(1)}_{N_{1}} \end{bmatrix}, \]
em que \(N_1\) representa o número de neurônios dessa camada (\(N_1=3\) no exemplo). Para levar em conta os biases e obter uma formulação matricial, é conveniente definir
\[ \mathbf{x}^{(2)}=\left[\begin{array}{c} 1 \\ \mathbf{y}^{(1)} \end{array} \right] \]
para denotar o vetor de entrada da camada 2. A seguir, detalhamos o cálculo do vetor de saída da camada 2, ou seja, \(\mathbf{y}^{(2)}\).
Vamos reunir os biases e os pesos da camada 2 na seguinte matriz
\[\begin{align*} \mathbf{W}^{(2)} = \begin{bmatrix} {\color{blue}b^{(2)}_1} & {\color{blue}w_{11}^{(2)}} & {\color{blue}w_{12}^{(2)}} & {\color{blue}w_{13}^{(2)}}\\ {\color{red}b^{(2)}_2} & {\color{red}w_{21}^{(2)}} & {\color{red}w_{22}^{(2)}} & {\color{red}w_{23}^{(2)}}\\ \end{bmatrix}_{2\times 4} \triangleq \begin{bmatrix} {\color{blue}\mathbf{w}_{1}^{(2)}} \\ {\color{red}\mathbf{w}_{2}^{(2)}}\\ \end{bmatrix}. \end{align*}\]
O bias e os pesos em azul da primeira linha da matriz \(\mathbf{W}^{(2)}\), que correspondem aos elementos do vetor linha \({\mathbf{w}_{1}^{(2)}}\), são utilizados no cálculo da saída do neurônio 1 dessa camada. Já o bias e os pesos em vermelho da segunda linha são utilizados no cálculo da saída do neurônio 2. Observe que, diferente da formulação do neurônio utilizada até o momento, definimos os vetores contendo o bias e os pesos de cada neurônio da camada \(j\), ou seja, \(\mathbf{w}_k^{(j)}\), \(k=1, 2, \ldots, N_j\), como vetores linha e não como vetores coluna. Dessa forma, podemos escrever
\[\begin{align*} \mathbf{v}^{(2)} = \begin{bmatrix} {\color{blue}v^{(2)}_1} \\ {\color{red}v^{(2)}_2}\\ \end{bmatrix} = \begin{bmatrix} {\color{blue}\mathbf{w}_1^{(2)}}\mathbf{x}^{(2)} \\ {\color{red}\mathbf{w}_2^{(2)}}\mathbf{x}^{(2)}\\ \end{bmatrix} =\mathbf{W}^{(2)}\mathbf{x}^{(2)} \;\;\textnormal{e}\;\; \mathbf{y}^{(2)} = \varphi_2(\mathbf{v}^{(2)})=\begin{bmatrix} {\color{blue}\varphi_2(v^{(2)}_1)} \\ {\color{red}\varphi_2(v^{(2)}_2)}\\ \end{bmatrix}= \begin{bmatrix} {\color{blue}y^{(2)}_1} \\ {\color{red}y^{(2)}_2} \\ \end{bmatrix}. \end{align*}\]
Generalizando, temos
\[\begin{align*} \mathbf{v}^{(j)} \triangleq \begin{bmatrix} v^{(j)}_1 \\ v^{(j)}_2 \\ \vdots \\ v^{(j)}_{N_{j}} \end{bmatrix},\;\;\; \mathbf{y}^{(j)} \triangleq \begin{bmatrix} y^{(j)}_1 \\ y^{(j)}_2 \\ \vdots \\ y^{(j)}_{N_{j}} \end{bmatrix} \;\; \text{e} \;\; \mathbf{x}^{(j)}\triangleq \begin{bmatrix} 1 \\ \mathbf{y}^{(j-1)} \end{bmatrix}, \end{align*}\]
em que \(j=1, 2, \ldots, L\), \(L\) é o número de camadas da rede e \(\mathbf{y}^{(0)}\) o vetor de entradas da rede. Definindo agora a matriz de pesos associados à camada \(j\) como
\[\begin{align*} \mathbf{W}^{(j)} \triangleq \begin{bmatrix} b^{(j)}_1 & w_{11}^{(j)} & w_{12}^{(j)} & \dots & w_{1N_{j - 1}}^{(j)}\\ b^{(j)}_2 & w_{21}^{(j)} & w_{22}^{(j)} & \dots & w_{2N_{j - 1}}^{(j)}\\ \vdots & \vdots & \vdots & \ddots & \vdots\\ b_{N_j}^{(j)} & w_{N_{j}1}^{(j)} & w_{N_{j}2}^{(j)} & \dots & w_{N_{j}N_{j - 1}}^{(j)} \end{bmatrix}_{(N_{j})\times (N_{j - 1}+1)} = \begin{bmatrix} \mathbf{w}_{1}^{(j)} \\ \mathbf{w}_{2}^{(j)} \\ \vdots \\ \mathbf{w}_{N_{j}}^{(j)}\\ \end{bmatrix}, \end{align*}\]
o vetor de saída dos combinadores lineares da camada \(j\) é dado por
\[\begin{equation*} \mathbf{v}^{(j)} = \left[\begin{array}{c} \mathbf{w}_1^{(j)}\mathbf{x}^{(j)} \\ \mathbf{w}_2^{(j)}\mathbf{x}^{(j)} \\ \vdots \\ \mathbf{w}_{N_j}^{(j)}\mathbf{x}^{(j)} \end{array} \right]= \mathbf{W}^{(j)}\mathbf{x}^{(j)}. \end{equation*}\]
Por fim, o vetor de saída dessa camada é calculado como
\[\begin{equation*} \mathbf{y}^{(j)} = \varphi_j\left(\mathbf{v}^{(j)}\right), \end{equation*}\]
em que a função de ativação \(\varphi_j\left(\cdot\right)\) é aplicada a cada elemento do vetor \(\mathbf{v}^{(j)}\).
O cálculo apresentado até aqui é utilizado para obter as saídas dos neurônios de cada camada da rede. Como o cálculo das saídas da camada \(j\) depende das saídas da camada \((j-1)\), dizemos que o cálculo é progressivo. Uma vez calculada a saída da rede, podemos compará-la com o sinal desejado e utilizar esse resultado para atualizar os pesos e os biases a fim de minimizar uma função custo, como veremos a seguir.
O algoritmo de retropropagação
O algoritmo de retropropagação (backpropagation) é o mais utilizado no processo de aprendizado supervisionado das redes neurais. Ele é dividido em duas etapas, descritas a seguir.
Cálculo progressivo
Nessa etapa, os pesos e biases são mantidos fixos e o cálculo é realizado progressivamente até se obter o vetor de saída \(\textbf{y}^{(L)}\). Nesse cálculo, a entrada é propagada ao longo da rede, camada por camada, como detalhado na seção anterior.
Cálculo regressivo
Nessa etapa, os pesos e biases são atualizados com o objetivo de minimizar uma função custo. Apesar de existirem diferentes funções custo, vamos nos concentrar por ora apenas no erro quadrático médio (MSE - mean square error), definido como
\[ J_{\rm MSE}=\frac{1}{N_L}\sum_{\ell=1}^{N_L}e^2_\ell(n) \]
em que
\[ e_\ell(n)=d_\ell(n)-y_\ell^{(L)}(n) \]
são os erros dos neurônios da camada de saída da rede. Para simplificar a dedução, vamos considerar o modo de treinamento estocástico em que os pesos e biases são atualizados a cada dado de treinamento \(n=1, 2, \ldots, N_t.\)
Utilizando o método do gradiente estocástico, a matriz de pesos da camada \(j\) pode ser atualizada como
\[\begin{equation*} \textbf{W}^{(j)}(n) = \textbf{W}^{(j)}(n-1) - \eta \frac{\partial J_{MSE}}{\partial \textbf{W}^{(j)}(n-1)}, \end{equation*}\]
em que \(\eta\) é um passo de adaptação e
\[ \frac{\partial J_{MSE}}{\partial \textbf{W}^{(j)}(n\!-\!1)}= \begin{bmatrix} \frac{\partial J_{MSE}}{\partial b^{(j)}_1(n\!-\!1)} & \frac{\partial J_{MSE}}{\partial w_{11}^{(j)}(n\!-\!1)} & \frac{\partial J_{MSE}}{\partial w_{12}^{(j)}(n\!-\!1)} & \dots & \frac{\partial J_{MSE}}{\partial w_{1N_{j - 1}}^{(j)}(n\!-\!1)}\\ \frac{\partial J_{MSE}}{\partial b^{(j)}_2(n\!-\!1)} & \frac{\partial J_{MSE}}{\partial w_{21}^{(j)}(n\!-\!1)} & \frac{\partial J_{MSE}}{\partial w_{22}^{(j)}(n\!-\!1)} & \dots & \frac{\partial J_{MSE}}{\partial w_{2N_{j - 1}}^{(j)}(n\!-\!1)}\\ \vdots & \vdots & \vdots & \ddots & \vdots\\ \frac{\partial J_{MSE}}{\partial b_{N_j}^{(j)}(n\!-\!1)} & \frac{\partial J_{MSE}}{\partial w_{N_{j}1}^{(j)}(n\!-\!1)} & \frac{\partial J_{MSE}}{\partial w_{N_{j}2}^{(j)}(n\!-\!1)} & \dots & \frac{\partial J_{MSE}}{\partial w_{N_{j}N_{j - 1}}^{(j)}(n\!-\!1)} \end{bmatrix}. \]
Observe que na \(k\)-ésima linha dessa matriz, temos o vetor gradiente2
\[ \boldsymbol{\nabla}_{\mathbf{w}_k^{(j)}}J_{\rm MSE}= \frac{\partial J_{\rm MSE}}{\partial \mathbf{w}_k^{(j)}(n-1)}= \begin{bmatrix} \frac{\partial J_{MSE}}{\partial b^{(j)}_k(n\!-\!1)} & \frac{\partial J_{MSE}}{\partial w_{k1}^{(j)}(n\!-\!1)} & \frac{\partial J_{MSE}}{\partial w_{k2}^{(j)}(n\!-\!1)} & \dots & \frac{\partial J_{MSE}}{\partial w_{kN_{j - 1}}^{(j)}(n\!-\!1)}\end{bmatrix}. \]
Assim, podemos escrever
\[ \frac{\partial J_{MSE}}{\partial \textbf{W}^{(j)}(n\!-\!1)}=\begin{bmatrix} \boldsymbol{\nabla}_{\mathbf{w}_1^{(j)}}J_{MSE} \\ \boldsymbol{\nabla}_{\mathbf{w}_2^{(j)}}J_{MSE} \\ \vdots \\ \boldsymbol{\nabla}_{\mathbf{w}_{N_j}^{(j)}}J_{MSE} \end{bmatrix}. \]
Vamos calcular os vetores gradientes considerando os neurônios da camada de saída, ou seja, \(j=L\). Usando a regra da cadeia sucessivas vezes, obtemos
\[\begin{equation*} \begin{aligned}[b] \boldsymbol{\nabla}_{\mathbf{w}_k^{(L)}}J_{MSE}& = \frac{\partial J_{\rm MSE}}{\partial \textbf{w}_k^{(L)}(n-1)}=\frac{1}{N_L}\sum_{\ell=1}^{N_L}\frac{\partial e_{\ell}^2(n)}{\partial \textbf{w}_k^{(L)}(n-1)}=\frac{1}{N_L}\frac{\partial e_{k}^2(n)}{\partial \textbf{w}_k^{(L)}(n-1)}\\ &= \frac{1}{N_L}\;\frac{\partial e_k^2(n)}{\partial y_k^{(L)}(n)}\; \frac{\partial y_k^{(L)}(n)}{\partial v^{(L)}_k(n)}\; \frac{\partial v^{(L)}_k(n)}{\partial \textbf{w}_k^{(L)}(n-1)} \\ & = \frac{1}{N_L}\; 2 e_k(n)\; \frac{\partial [d_k(n)-y_k^{(L)}(n)]}{\partial y_k^{(L)}(n)}\; \frac{\partial \varphi_L\left(v^{(L)}_k(n)\right)}{\partial v^{(L)}_k(n)}\; \frac{\partial \textbf{w}^{(L)}_k(n-1)\,\textbf{x}^{(L)}(n)}{\partial \textbf{w}^{(L)}_k(n-1)} \\ & = -\frac{2}{N_L}\; e_k(n)\; \varphi_L'\!\left(v^{(L)}_k(n)\right) \; [\textbf{x}^{(L)}(n)]^{\rm T}, \end{aligned}\nonumber \label{chain_rule_w} \end{equation*}\]
em que \(\varphi_L'(\cdot)\) representa a derivada da função de ativação \(\varphi_L(\cdot)\), o que justifica a importância dessa função ser derivável em todos os pontos.
Definindo o gradiente local da camada \(L\) como
\[ \delta_{k}^{(L)}(n)\triangleq \varphi_L'(v_{k}^{(L)}(n))e_{k}(n), \]
o vetor gradiente pode ser reescrito como
\[ \boldsymbol{\nabla}_{\mathbf{w}_k^{(L)}}J_{MSE}= -\frac{2}{N_L}\; \delta_{k}^{(L)}(n) \; [\textbf{x}^{(L)}(n)]^{\rm T}. \]
Uma vez calculados os gradientes da camada de saída \(L\), podemos calcular os gradientes da última camada oculta, ou seja, para \(j=L-1\). Assim,
\[ \boldsymbol{\nabla}_{\mathbf{w}_k^{(L-1)}}J_{\rm MSE} = \frac{\partial J_{\rm MSE}}{\partial \mathbf{w}_k^{(L-1)}(n-1)}= \frac{1}{N_L}\;\sum_{\ell=1}^{N_L}\frac{\partial e_\ell^2(n)}{\partial \mathbf{w}_k^{(L-1)}(n-1)}. \]
Novamente, usando a regra da cadeia sucessivas vezes, obtemos
\[\begin{align*} \frac{\partial e_\ell^2(n)}{\partial \textbf{w}_k^{(L-1)}(n-1)}&=2 e_{\ell}(n)\frac{\partial [d_{\ell}(n)-y_{\ell}^{(L)}(n)]}{\partial y_{\ell}^{(L)}(n)} \frac{\partial y_{\ell}^{(L)}(n)}{\partial \textbf{w}_k^{(L-1)}(n-1)}\\ &=-2e_{\ell}(n)\frac{\partial \varphi_L(v_{\ell}^{(L)}(n))}{\partial v_{\ell}^{(L)}(n)}\frac{\partial v_{\ell}^{(L)}(n)}{\partial \textbf{w}_k^{(L-1)}(n-1)}. \end{align*}\]
Observe que
\[ v_{\ell}^{(L)}(n)=\mathbf{w}_{\ell}^{(L)}(n-1)\mathbf{x}^{(L)}(n)=b_{\ell}^{(L)}(n-1)+\sum_{m=1}^{N_{L-1}}w_{\ell m}^{(L)}(n-1)y_m^{(L-1)}(n). \]
No cálculo de \(v_{\ell}^{(L)}(n)\), o único termo que depende de \(\textbf{w}_k^{(L-1)}(n-1)\) é \(w_{\ell k}^{(L)}(n-1)y_k^{(L-1)}(n)\), já que a saída \(y_k^{(L-1)}(n)\) é calculada utilizando os pesos \(\textbf{w}_k^{(L-1)}(n-1)\). Assim, obtemos
\[\begin{align*} \frac{\partial e_\ell^2(n)}{\partial \textbf{w}_k^{(L-1)}(n-1)}&=-2e_{\ell}(n)\varphi_L'(v_{\ell}^{(L)}(n))w_{\ell k}^{(L)}(n-1)\frac{\partial y_{k}^{(L-1)}(n)}{\partial \textbf{w}_k^{(L-1)}(n-1)}\\ &=-2e_{\ell}(n)\varphi_L'(v_{\ell}^{(L)}(n))w_{\ell k}^{(L)}(n-1)\frac{\partial \varphi_{L-1}(v_{k}^{(L-1)}(n))}{\partial v_{k}^{(L-1)}(n)}\frac{\partial v_{k}^{(L-1)}(n)}{\partial \textbf{w}_k^{(L-1)}(n-1)}\\ &=-2e_{\ell}(n)\varphi_L'(v_{\ell}^{(L)}(n))w_{\ell k}^{(L)}(n-1)\varphi_{L-1}'(v_{k}^{(L-1)}(n))\frac{\partial \mathbf{w}_{k}^{(L-1)}(n-1)\mathbf{x}^{(L-1)}(n)} {\partial \textbf{w}_k^{(L-1)}(n-1)}\\ &=-2e_{\ell}(n)\varphi_L'(v_{\ell}^{(L)}(n))w_{\ell k}^{(L)}(n-1)\varphi_{L-1}'(v_{k}^{(L-1)}(n))[\mathbf{x}^{(L-1)}(n)]^{\rm T}. \end{align*}\]
Identificando \(\delta^{(L)}_{\ell}(n)\) na expressão anterior e substituindo o resultado na expressão do gradiente, obtém-se
\[ \boldsymbol{\nabla}_{\mathbf{w}_k^{(L-1)}}J_{\rm MSE} = -\frac{2}{N_L}\;\varphi_{L-1}'(v_{k}^{(L-1)}(n))\;\sum_{\ell=1}^{N_L}\delta_{\ell}^{(L)}(n)w_{\ell k}^{(L)}(n-1)[\mathbf{x}^{(L-1)}(n)]^{\rm T}. \]
Definindo agora o gradiente local da camada \(L-1\) como
\[ \delta_{k}^{(L-1)}(n)\triangleq \varphi_{L-1}'(v_{k}^{(L-1)}(n))\;\sum_{\ell=1}^{N_L}\delta_{\ell}^{(L)}(n)w_{\ell k}^{(L)}(n-1), \]
o vetor gradiente pode ser reescrito como
\[ \boldsymbol{\nabla}_{\mathbf{w}_k^{(L-1)}}J_{\rm MSE} = -\frac{2}{N_L}\delta_{k}^{(L-1)}(n)[\mathbf{x}^{(L-1)}(n)]^{\rm T}. \]
Comparando a expressão do gradiente local \(\delta_{k}^{(L-1)}(n)\) da camada \(L-1\) com a expressão do gradiente local \(\delta_{k}^{(L)}(n)\) da camada \(L\), o somatório
\[ \sum_{\ell=1}^{N_L}\delta_{\ell}^{(L)}(n)w_{\ell k}^{(L)}(n-1) \]
faz o papel de erro do neurônio \(k\) da camada \(L-1\). Essa retropropagação dos erros deve continuar até a primeira camada oculta. O fluxo do sinal na retropropagação para as camadas \(L\) e \(L-1\) está esquematizado na Figura 3. O erro do neurônio \(k\) da camada \(L-1\) é o sinal obtido no ponto indicado pelo círculo azul na figura.
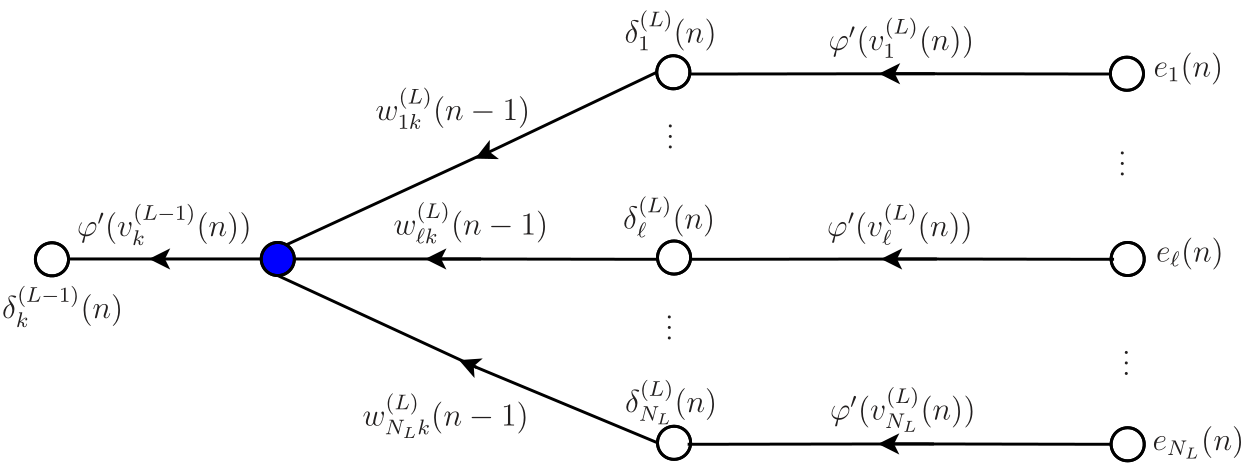
Generalizando, define-se o gradiente local para qualquer camada oculta \(j\) como
\[\begin{equation*} \fbox{$\displaystyle \delta_{k}^{(j)}(n)\triangleq \varphi_j'(v_{k}^{(j)}(n))\;\sum_{\ell=1}^{N_{j+1}}\delta_{\ell}^{(j+1)}(n)w_{\ell k}^{(j+1)}(n-1) $} \end{equation*}\]
e para a camada de saída \(L\) como
\[\begin{equation*} \fbox{$\displaystyle \delta_{k}^{(L)}(n)\triangleq \varphi_L'(v_{k}^{(L)}(n))e_k(n). $} \end{equation*}\]
Definindo os vetores
\[ \boldsymbol{\delta}^{(j)}(n)\triangleq \left[\begin{array}{c} \delta_{1}^{(j)}(n) \\ \delta_{2}^{(j)}(n) \\ \vdots \\ \delta_{N_j}^{(j)}(n) \end{array} \right],\;\;\; \mathbf{e}(n)\triangleq \left[\begin{array}{c} e_{1}(n) \\ e_{2}(n) \\ \vdots \\ e_{N_L}(n) \end{array}\right],\;\;\; \mathbf{d}_{\varphi}^{(j)}(n)\triangleq \left[\begin{array}{c} \varphi_j'(v_1^{(j)}(n)) \\ \varphi_j'(v_2^{(j)}(n)) \\ \vdots \\ \varphi_j'(v_{N_j}^{(j)}(n)) \end{array}\right] \]
e a matriz \(\overline{\mathbf{W}}^{(j+1)}(n-1)\) excluíndo a coluna de biases da matriz \({\mathbf{W}}^{(j+1)}(n-1)\), ou seja,
\[ \overline{\mathbf{W}}^{(j+1)}(n-1)\triangleq \begin{bmatrix} w_{11}^{(j+1)}(n-1) & w_{12}^{(j+1)}(n-1) & \dots & w_{1N_{j}}^{(j+1)}(n-1)\\ w_{21}^{(j+1)}(n-1) & w_{22}^{(j+1)}(n-1) & \dots & w_{2N_{j}}^{(j+1)}(n-1)\\ \vdots & \vdots & \ddots & \vdots\\ w_{N_{j+1}1}^{(j+1)}(n-1) & w_{N_{j+1}2}^{(j+1)}(n-1) & \dots & w_{N_{j+1}N_{j}}^{(j+1)}(n-1) \end{bmatrix}_{N_{j+1}\times N_{j}}, \] podemos escrever para a camada de saída
\[\begin{equation*} \fbox{$\displaystyle \boldsymbol{\delta}^{(L)}(n)=\nonumber\mathbf{d}_{\varphi}^{(L)}(n)\odot\mathbf{e}(n) $} \end{equation*}\]
e para as camadas ocultas
\[\begin{equation*} \fbox{$\displaystyle \boldsymbol{\delta}^{(j)}(n)=\nonumber\mathbf{d}_{\varphi}^{(j)}(n)\odot\left\{\left[\overline{\mathbf{W}}^{(j+1)}(n-1)\right]^{\rm T}\;\boldsymbol{\delta}^{(j+1)}(n)\right\}\nonumber $} \end{equation*}\]
em que \(\odot\) representa a multiplicação elemento por elemento entre dois vetores. Essa forma de calcular os vetores de gradientes locais é mais eficiente, já que todos os elementos são calculados de uma vez em cada camada .
É comum incorporar a constante \(2/N_L\) que aparece nos cálculos dos gradientes ao passo de adaptação \(\eta\). Dessa forma, as equações de atualização dos vetores de pesos do neurônio \(k\) da camada \(j\) podem ser escritas como
\[\begin{equation*} \fbox{$\displaystyle \mathbf{w}_{k}^{(j)}(n)=\mathbf{w}_{k}^{(j)}(n-1)+\eta\delta_{k}^{(j)}(n)[\mathbf{x}^{(j)}(n)]^{\rm T} $} \end{equation*}\]
\(k=1, 2, \ldots, N_j\;\;,\) \(j=1, 2 \ldots, L\). Definindo a matriz
\[ \boldsymbol{\Delta}_{\delta}^{(j)}(n)=\boldsymbol{\delta}^{(j)}(n)[\mathbf{x}^{(j)}(n)]^{\rm T} \]
podemos atualizar a matriz de pesos da camada \(j\) como
\[\begin{equation*} \fbox{$\displaystyle \mathbf{W}^{(j)}(n)=\mathbf{W}^{(j)}(n-1)+\eta\boldsymbol{\Delta}_{\delta}^{(j)}(n). $} \end{equation*}\]
Como a implementação matricial é mais eficiente, essa forma de atualização é preferida. Os pesos e biases precisam ser inicializados. No LMS, esses parâmetros são geralmente inicializados com zero. No entanto, se fizermos o mesmo no algoritmo backpropagation, dependendo da função de ativação, esses parâmetros não serão atualizados. Para exemplificar, vamos considerar a tangente hiperbólica como função de ativação. Essa função é definida como
\[ \varphi_j(v)={\rm tanh}(v)=\frac{e^v-e^{-v}}{e^v+e^{-v}}. \]
Note que se inicializarmos os pesos e biases com zero, as saídas dos combinadores lineares dos neurônios também serão iguais zero e como \({\rm tanh}(0)=0\), as saídas dos neurônios e consequentemente os gradientes serão nulos. Dessa forma, não ocorre atualização dos pesos e biases. Em geral, não temos nenhuma informação prévia sobre a solução “ótima” dos pesos e biases. Por isso, costuma-se inicializar esses parâmetros a partir de uma distribuição uniforme. O intervalo da distribuição depende do problema. Podemos considerar, por exemplo, valores uniformemente distribuídos no intervalo \([-10^{-2}, 10^{-2}]\).
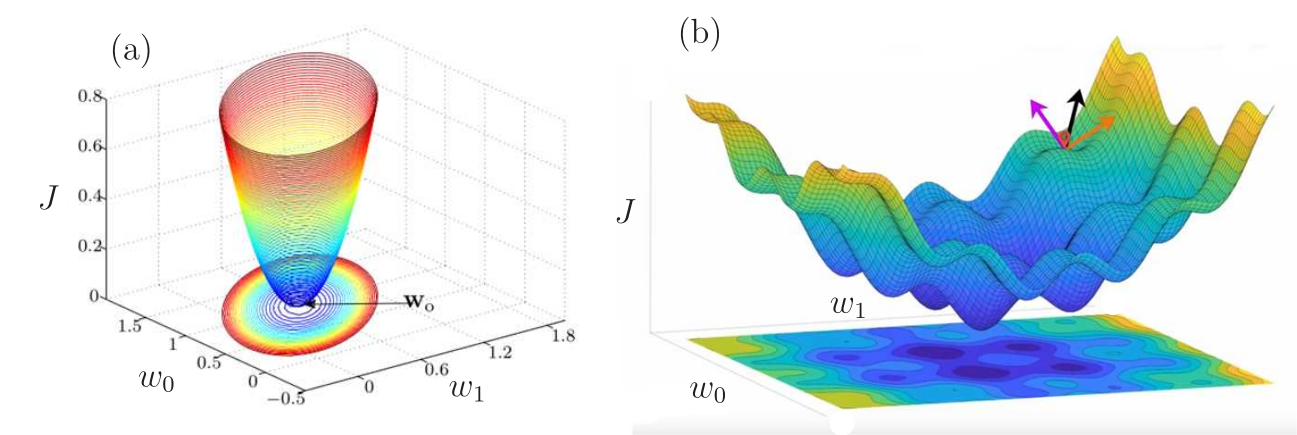
Diferente do que acontece no algoritmo LMS, a função custo minimizada pelo algoritmo backpropagation tem inúmeros mínimos locais devido às não linearidades inseridas pelas funções de ativação. Suponha hipoteticamente que temos apenas dois parâmetros \(w_0\) e \(w_1\) a serem ajustados. Na Figura 4 (a) temos o MSE a ser minimizado pelo LMS, que apresenta um único ponto de mínimo, que é a solução de Wiener como vimos anteriormente. Já na Figura 4 (b), temos uma função custo com inúmeros mínimos locais. Não temos mais uma função convexa e o gradiente é nulo nesses pontos de mínimo. Isso faz com que o algoritmo pare de atualizar e atinja uma solução subótima, que por sua vez, pode estar muito distante do mínimo global da função custo. Vários fatores fazem com que o algoritmo backpropagation pare em um mínimo local: o passo de adaptação, a inicialização, determinadas funções de ativação, etc. A solução subótima nem sempre é adequada. Por isso, várias soluções para fazer com que o algoritmo saia dos mínimos locais foram propostas na literatura como veremos posteriormente.
No Algoritmo 1, é apresentado o pseudocódigo do algoritmo backpropagation no modo de treinamento estocástico. Apesar da dedução ter sido feita neste modo, ele raramente é utilizado de forma estocástica. Em vez disso, é mais comum considerar os modos de treinamento batch e mini-batch. Como fizemos a formulação desses modos no algoritmo LMS, sua extensão para o backpropagation é direta e deixaremos a cargo do leitor.
Exemplo 1 Sumário do algoritmo backpropagation para treinamento da rede MLP no modo estocástico. \(N_t\) é o número de dados de treinamento.
Inicialização: as matrizes \(\mathbf{W}^{(j)}(0),\;j=1,2,\ldots, L\) devem ser inicializadas com números aleatórios uniformemente distribuídos
Para \(n=1,2,\ldots,\) calcule:
Cálculo progressivo
\(\mathbf{y}^{(0)} = [y_{1}\; y_{2}\;\cdots\; y_{N_0}]^{\rm T} = [x_{1n}\; x_{2n}\;\cdots\; x_{N_0n}]^{\rm T}\)
Para \(j=1,2,\ldots, L,\) calcule:
\(\mathbf{x}^{(j)}(n)=\left[\begin{array}{c}
1 \\
\mathbf{y}^{(j-1)}(n)\\
\end{array}
\right]\)
\(\mathbf{v}^{(j)}(n)=\mathbf{W}^{(j)}(n-1)\mathbf{x}^{(j)}(n)\)
\(\mathbf{y}^{(j)}(n)=\varphi_j(\mathbf{v}^{(j)}(n))\)
\(\mathbf{d}_{\varphi}^{(j)}(n)=\varphi_j'(\mathbf{v}^{(j)}(n))\)
Fim
\(\mathbf{e}(n)=\mathbf{d}(n)-\mathbf{y}^{(L)}(n)\)
Cálculo regressivo
Para \(j=L,L-1,\ldots, 1,\) calcule:
Se \(j=L\)
\(\boldsymbol{\delta}^{(j)}(n)=\mathbf{d}_{\varphi}^{(L)}(n)\odot \mathbf{e}(n)\)
Caso contrário
\(\boldsymbol{\delta}^{(j)}(n)=\mathbf{d}_{\varphi}^{(j)}(n)\odot\left\{\left[\overline{\mathbf{W}}^{(j+1)}(n-1)\right]^{\rm T}\;\boldsymbol{\delta}^{(j+1)}(n)\right\}\)
Fim
\(\boldsymbol{\Delta}_{\delta}^{(j)}(n)=\boldsymbol{\delta}^{(j)}(n) [\mathbf{x}^{(j)}(n)]^{T}\)
\(\mathbf{W}^{(j)}(n)=\mathbf{W}^{(j)}(n-1)+ \eta\boldsymbol{\Delta}_{\delta}^{(j)}(n)\)
Fim
Fim
Utilizando a rede MLP no problema das meias-luas
Vamos voltar ao exemplo de classificação das meias-luas com \(r_1=10\), \(r_2=-4\) e \(r_3=6\). Vimos que essa situação exigia uma separação não linear que tanto o algoritmo LMS quanto o perceptron de Rosenblatt não são capazes de fornecer. Vamos considerar agora a solução obtida por uma rede MLP com a seguinte configuração \(2\)-\(3(\text{tanh})\)-\(2(\text{tanh})\)-\(1(\text{tanh})\) no modo de treinamento mini-batch (\(N_0=2\), \(N_t=1000\), \(N_b=50\) e \(N_e=10^4\)). Os pesos e biases foram inicializados com números aleatórios gerados a partir de uma distribuição uniforme no intervalo \([-10^{-2}, 10^{-2}]\) e o passo de adaptação foi considerado fixo e igual a \(\eta=0,\!1\). Considerou-se ainda a função custo do erro quadrático médio (MSE).
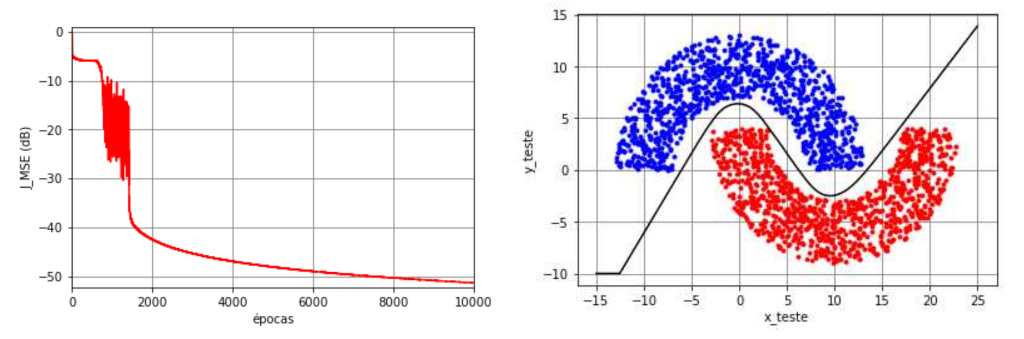
Na Figura 5 são mostradas a função custo ao longo das épocas, a classificação dos dados de teste e a separação das regiões. Observa-se que a função custo não terminou de convergir apesar das \(N_e=10^4\) épocas. No entanto, o valor que ela atinge na última época é de aproximadamente \(J_{\rm MSE}\approx 9,7 \times 10^{-6}\), o que corresponde a \(-50,\!1~\text{dB}\). Caso não tenha ocorrido overfitting, esse valor é baixo o suficiente para conseguir separar adequadamente as regiões. Para comprovar, foram gerados \(N_{\rm teste}=2000\) dados de teste que foram classificados pela MLP considerando os pesos e os biases da última iteração. Podemos observar na figura que não há erros de classificação (taxa de erro igual a zero) e a separação obtida é não linear, como esperado.
Para ilustrar a evolução da fronteira de decisão ao longo das épocas, a classificação dos dados de teste e a separação das regiões são mostradas na Figura 6 para diferentes valores de \(N_e\). Para cada caso, os pesos obtidos na época em questão foram considerados fixos e usados para classificação dos dados de teste. As respectivas taxas de erro estão mostradas na Tabela 1. Nota-se que \(N_e=5\) épocas é muito pouco para que a MLP consiga classificar os dados. A medida que o número de épocas aumenta, a separação vai tomando uma forma mais adequada, o que faz com que a taxa de erros diminua, como esperado. Para \(N_e=400\), a taxa de erros é de 1,65% e para \(N_e=500\) não há mais erros de classificação. Diante disso, \(500\) épocas são suficientes para que a MLP consiga classificar corretamente os dados.
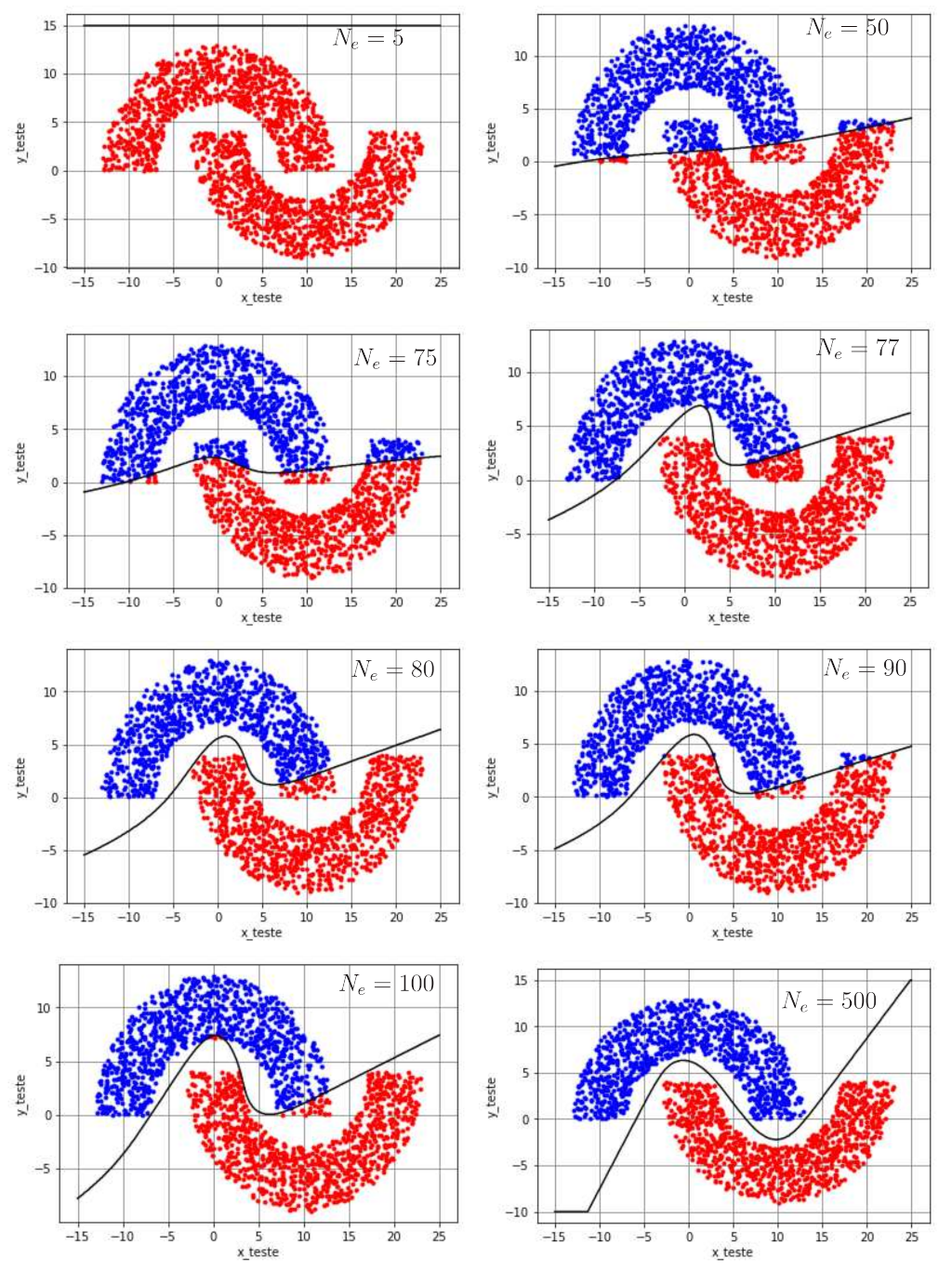
| \(N_e\) | Taxa de erro (%) |
|---|---|
| 5 | 50,00 |
| 9 | 17,05 |
| 50 | 11,95 |
| 200 | 10,65 |
| 250 | 10,08 |
| 300 | 9,00 |
| 400 | 1,65 |
| 500 | 0,00 |
Apesar do excelente resultado da Figura 5, nenhuma técnica foi utilizada para fazer com que o algoritmo backpropagation não ficasse parado em mínimos locais. Ao inicializar os pesos e biases considerando a mesma distribuição mas sorteando valores diferentes, é possível que o algoritmo fique parado em mínimos locais que levam a soluções subótimas. Essa situação pode ser observada na Figura 7. Observa-se que a função custo atinge aproximadamente \(J_{\rm MSE}\approx 0,18\), o que corresponde a \(-7,4\) dB. Apesar da separação não linear, há vários pontos da Região A (azul) classificados erroneamente como pertencentes à Região B (vermelha), o que leva a uma taxa de erros de \(7,\!8\%\).
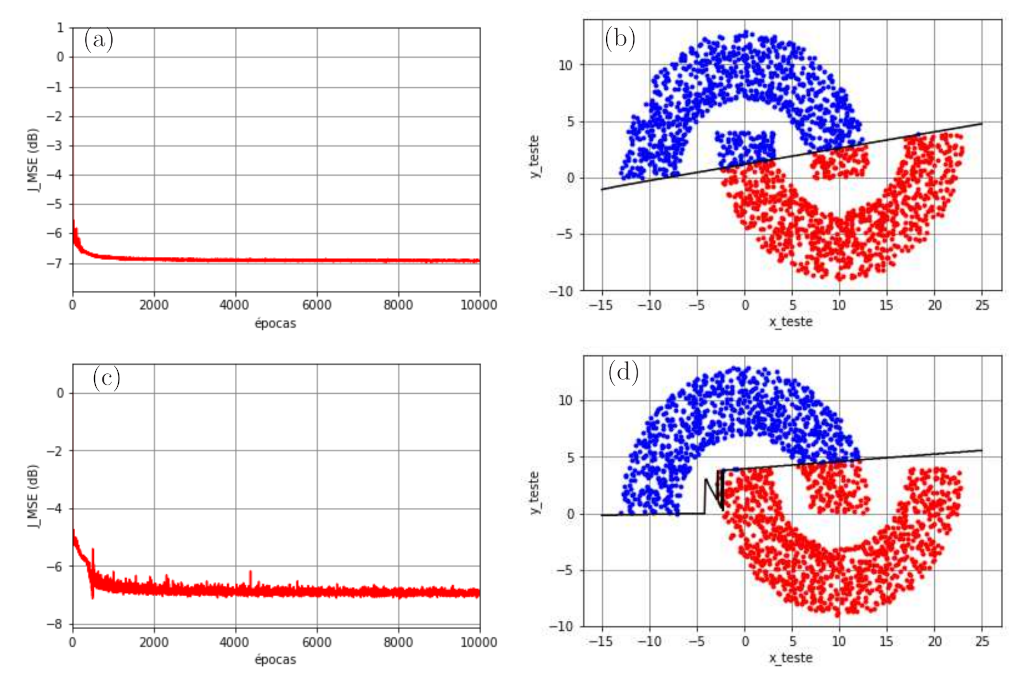
A conclusão desse exemplo é que a rede MLP é capaz de proporcionar soluções não lineares que podem ser adequadas a vários problemas de classificação e regressão. No entanto, é importante utilizar técnicas que façam com que o algoritmo backpropagation não fique parado em mínimos locais. Antes de discutirmos essas técnicas, vamos abordar a seguir o Teorema de Cybenko que diz que a MLP é um aproximador universal de funções.
MLP como aproximador universal de funções
Uma rede MLP treinada com o algoritmo backpropagation pode ser vista como um sistema capaz de realizar um mapeamento entrada-saída de forma não linear. Considere uma rede MLP com \(N_0\) entradas e \(N_L\) saídas. A relação entrada-saída da rede define um mapeamento de um espaço Euclidiano de entrada de dimensão \(N_0\) a um espaço Euclidiano de saída de dimensão \(N_L\), que é infinitamente e continuamente diferenciável desde que a função de ativação também seja. Neste contexto, cabe a seguinte pergunta: qual o número mínimo de camadas ocultas que a rede MLP precisa ter para fornecer uma aproximação de qualquer mapeamento contínuo? A resposta para essa pergunta envolve o Teorema da Aproximação Universal, enunciado a seguir.
Seja \(\varphi(\cdot)\) uma função contínua, não constante, limitada e monotônica crescente. Vamos utilizar \(I_{N_0}\) para denotar o hipercubo unitário \([0,\;1]^{N_0}\) de dimensão \(N_0\). O espaço de funções contínuas em \(I_{N_0}\) é denotado por \(C(I_{N_0})\). Então, dada qualquer função \(f \in C(I_{N_0})\) e \(\varepsilon>0\), existe um inteiro \(N_1\) e conjuntos de constantes reais \(\alpha_i\), \(b_i\) e \(w_{ij}\), \(i=1, 2, \ldots, N_1\) e \(j=1, 2, \ldots,N_0\) tal que se pode definir
\[ F(x_1, x_2, \ldots, x_{N_0})=\displaystyle\sum_{i=1}^{N_1}\alpha_i\varphi\left(\displaystyle\sum_{j=1}^{N_0}w_{ij}x_j+b_i\right) \]
como uma aproximação da função \(f(\cdot)\), ou seja,
\[ |F(x_1, x_2, \ldots, x_{N_0})-f(x_1, x_2, \ldots, x_{N_0})|<\varepsilon \]
para todos \(x_1, x_2, \ldots, x_{N_0}\) do espaço de entrada.
O Teorema da Aproximação Universal é diretamente aplicável à rede MLP. Primeiramente, cabe observar que a tangente hiperbólica, comumente usada como função de ativação, é não constante, limitada e monotonicamente crescente. Portanto, ela satisfaz as condições impostas para a função \(\varphi(\cdot)\). Além disso,
\[ \displaystyle\sum_{i=1}^{N_1}\alpha_i\varphi\left(\displaystyle\sum_{j=1}^{N_0}w_{ij}x_j+b_i\right) \]
representa a saída de uma MLP descrita a seguir:
- a rede possui \(N_0\) entradas, indicadas por \(x_1, x_2, \ldots, x_{N_0}\), e uma única camada oculta composta por \(N_1\) neurônios;
- o neurônio oculto \(i\) tem pesos \(w_{i1}, w_{i2}, \ldots, w_{iN_0}\) e bias \(b_i\);
- a saída da rede é uma combinação linear das saídas dos neurônios ocultos, com \(\alpha_1\), \(\alpha_2, \ldots,\) \(\alpha_{N_1}\) sendo os pesos da saída.
A partir desse teorema, pode-se afirmar que uma única camada oculta é suficiente para que uma rede MLP obtenha uma aproximação uniforme para um determinado conjunto de treinamento, representado pelas entradas \(x_1, x_2, \ldots, x_{N_0}\), e uma saída desejada \(f(x_1, x_2, \ldots, x_{N_0})\). Por isso, as redes MLP são conhecidas como aproximadores universais de funções. Esse resultado foi demonstrado pela primeira vez por Cybenko em 1988 e por isso, também é chamado de Teorema de Cybenko na literatura de redes neurais. Apesar desse resultado interessante, o teorema não nos diz que uma única camada oculta é ótima no sentido de tempo de aprendizado, simplicidade de implementação ou capacidade de generalização. Mais detalhes podem ser encontrados, por exemplo, em (Haykin 2009).
Referências
Notas de rodapé
Em alguns livros, considera-se também a entrada como uma camada, como é o caso, por exemplo, da formulação de (Haykin 2009). Aqui, vamos considerar camadas apenas as que possuem neurônios. Dessa forma, a primeira camada da rede MLP será sempre oculta.↩︎
Como passamos a considerar os vetores de pesos e bias como vetores linha, o vetor gradiente correspondente também é linha.↩︎