Exemplo MLP com PyTorch

Segue a implementação comentada em PyTorch da MLP para solução do problemas das meias luas, equivalente ao código implementado manualmente no Exercício 5.

Iniciando com a importação das bibliotecas:

import numpy as np
import matplotlib.pyplot as plt

import torch
import torch.nn as nn

# Fixando seeds para poder reproduzir os resultados
np.random.seed(111)
torch.manual_seed(111)
torch.cuda.manual_seed(111)

Definindo a função para gerar dados para treinamento:

# Função para garar dados de treinamento
def meias_luas(NA, NB, r1, r2, r3):
    """
    dados = meias_luas(NA,NB,r1,r2,r3)
    NA: número de pontos da região A
    NB: número de pontos da região B
    r1, r2 e r3: dados das meias-luas
    """

    # total de dados de treinamento
    Nt = NA + NB

    # dados das meia luas
    rmin = r1 - r3 / 2
    rmax = r1 + r3 / 2

    # Pontos da Região A
    a = np.pi * np.random.rand(NA, 1)
    rxy = np.random.uniform(rmin, rmax, (NA, 1))
    x1A = rxy * np.cos(a)
    x2A = rxy * np.sin(a)
    dA = np.ones((NA, 1))
    pontosA = np.hstack((x1A, x2A, dA))

    # Pontos da Região B
    a = np.pi * np.random.rand(NB, 1)
    rxy = np.random.uniform(rmin, rmax, (NB, 1))
    x1B = rxy * np.cos(a) + r1
    x2B = -rxy * np.sin(a) - r2
    dB = -np.ones((NB, 1))    
    pontosB = np.hstack((x1B, x2B, dB))

    # Concatenando e embaralhando os dados
    dados = np.vstack((pontosA, pontosB))
    np.random.shuffle(dados)

    # Figura para mostrar os dados de treino
    fig, ax1 = plt.subplots()
    ax1.plot(x1A, x2A, ".b")
    ax1.plot(x1B, x2B, ".r")
    plt.xlabel("x_1")
    plt.ylabel("x_2")
    plt.grid(axis="x", color="0.5")
    plt.grid(axis="y", color="0.5")

    return dados

Em seguida, criando os dados para treinamento do modelo:

# Gerando dados de treinamento
# Note o uso do sufixo `_np` para facilitar a identificação
# de arrays do NumPy e não confundi-los com tensores do PyTorch

# número de pontos de treinamento da Região A
NA = 500

# número de pontos de treinamento da Região B
NB = 500

# número total de dados de treinamento
Nt = NA + NB

r1 = 10
r3 = 6
r2 = -4

dados_treino_np = meias_luas(NA, NB, r1, r2, r3)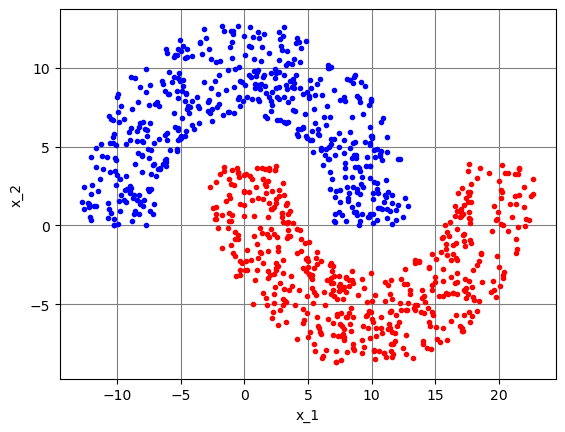

Ajustando os valores dos hiperparâmetros:

# Ajuste de hiperparâmetros

# passo de adaptação da rede MLP
eta = 0.5

# Tamanho do mini-batch
Nb = 100

# Número de épocas
Ne = 10000

O PyTorch utiliza um elemento chamado de DataLoader para facilitar o carregamento dos dados, embaralhamento e geração dos mini batches. Ele é criado a partir de um iterador, que contém pares de dados no formato (entrada, saída):

dados_treino = torch.tensor(dados_treino_np, dtype=torch.float32)
train_set = [
    (dados_treino[i, [0, 1]], dados_treino[i, [2]])
    for i in range(dados_treino.shape[0])
]

train_loader = torch.utils.data.DataLoader(train_set, batch_size=Nb, shuffle=True)

Vale notar alguns detalhes do código anterior:

• Os dados de treinamento são armazenados em um tensor chamado dados_treino, criado a partir do array NumPy chamado dados_treino_np. Por padrão, o PyTorch trabalha com precisão de 32 bits e o NumPy, com precisão de 64 bits. Dessa forma, pensando em trabalhar na precisão numérica padrão do PyTorch, é necessário especificar dtype=torch.float32 para criar um tensor com precisão de 32 bits a partir de um array com precisão de 64 bits;
• Nesse exemplo, o iterador usado para criar o DataLoader é chamado de train_set;
• Ao criar o DataLoader, é fornecido o tamanho do mini batch por meio do argumento batch_size e, nesse caso, o DataLoader será responsável por embaralhar os dados a cada época, de acordo com o argumento shuffle, configurado como True;

O modelo é definido por meio de uma classe que herda de nn.Module:

class Model(nn.Module):

    # Geralmente, os blocos da rede são definidos no método __init__()
    def __init__(self):
        # Necessário chamar __init__() da classe mãe
        super().__init__()
        
        # Uma das formas de se definir um modelo é a sequencial
        self.model = nn.Sequential(
            # Entrada com 2 elementos, conectada a 3 neurônios
            nn.Linear(2, 3),
            # Função de ativação Tanh
            nn.Tanh(),
            
            # Saídas de 3 neurônios conectadas a 5 neurônios
            nn.Linear(3, 5),
            nn.Tanh(),
            
            nn.Linear(5, 5),
            nn.Tanh(),
            
            nn.Linear(5, 2),
            nn.Tanh(),
            
            nn.Linear(2, 1),
            nn.Tanh(),            
        )

    # O método forward() define como é feito o cálculo progressivo
    # para obter a saída da rede, a partir da entrada x.
    # Nesse caso, como foi definido um modelo sequencial em
    # self.model, basta chamar self.model(x)
    def forward(self, x):
        output = self.model(x)
        return output

Uma das vantagens de se usar o PyTorch para desenvolver aplicações de aprendizado de máquina é a possibilidade do uso de GPUs para acelerar o processo computação de forma simples

Geralmente é criado um objeto chamado device que aponta para a GPU, caso ela exista ou para a CPU, caso contrário, como mostrado a seguir:

device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")    

Com esse objeto criado, basta chamar o método .to(device=device) de tensores ou modelos, para enviá-los à GPU, caso ela exista.

Tendo a classe do modelo definida, é necessário instanciar um objeto para representá-lo. Na linha a seguir, o modelo é instanciado e enviado à GPU com o método .to(), caso ela exista:

model = Model().to(device=device)

Definindo a função custo e o otimizador:

loss_function = nn.MSELoss()

optimizer = torch.optim.SGD(model.parameters(), lr=eta)

Nesse caso, utiliza-se a função custo do erro quadrático médio MSELoss e o otimizador baseado no gradiente descendente estocástico SGD. O PyTorch conta com uma série de outras fuções custo e otimizadores que podem ser utilizados. Para referência, consulte:

• Funções custo: https://pytorch.org/docs/stable/nn.html#loss-functions
• Otimizadores:https://pytorch.org/docs/stable/optim.html#algorithms

Um diferencial do PyTorch é que o treinamento deve ser feito explicitamente, com um loop para as épocas e outro para os mini batches:

# Lista usada para guardar o valor da função custo ao longo das iterações
losses = []

# Loop das épocas
for epoch in range(Ne):
    # Loop dos mini batches - note que é usado o DataLoader para obter
    # os sinais de entrada e desejado, X e d
    for n, (X, d) in enumerate(train_loader):

        # Envia os dados para a GPU, caso ela exista
        X = X.to(device=device)
        d = d.to(device=device)
        
        # Coloca o modelo em modo treinamento. Isso não é necessário nesse
        # caso, pois não estamos fazendo validação. Mas é interessante manter
        # a linha para lembrar desse detalhe
        model.train()

        # Zera informações de gradientes: por padrão o PyTorch acumula os 
        # gradientes a cada chamada de loss.backward(). Na maioria dos casos,
        # estamos interessados apenas no último valor dos gradientes
        model.zero_grad()
        
        # Calcula a saída
        y = model(X)

        # Calcula o valor da função custo
        loss = loss_function(y, d)
        
        # Calcula os gradientes
        loss.backward()
        
        # Atualiza os pesos do modelo, de acordo com as regras
        # do otimizador escolhido
        optimizer.step()
        
        # Armazena o valor da função custo
        losses.append(loss.item())
        
        # Mostra o valor da função custo a cada 500 épocas        
        if epoch % 500 == 0 and n == dados_treino.shape[0]//Nb - 1:
            print(f"Época: {epoch} Loss: {loss}")

plt.figure()
plt.plot(losses)
plt.xlabel("Batch")
plt.ylabel("Loss")

Época: 0 Loss: 0.7539945840835571
Época: 500 Loss: 0.0003208783164154738
Época: 1000 Loss: 1.0246196325169876e-05
Época: 1500 Loss: 5.569074801314855e-06
Época: 2000 Loss: 3.858567197312368e-06
Época: 2500 Loss: 2.9008722322032554e-06
Época: 3000 Loss: 2.3132092792366166e-06
Época: 3500 Loss: 1.960377858267748e-06
Época: 4000 Loss: 1.72843181189819e-06
Época: 4500 Loss: 1.5078306887517101e-06
Época: 5000 Loss: 1.387525685458968e-06
Época: 5500 Loss: 1.1053163007090916e-06
Época: 6000 Loss: 1.1061830491598812e-06
Época: 6500 Loss: 1.003904003482603e-06
Época: 7000 Loss: 9.989685167965945e-07
Época: 7500 Loss: 8.669725275467499e-07
Época: 8000 Loss: 8.007504561646783e-07
Época: 8500 Loss: 8.064585585998429e-07
Época: 9000 Loss: 7.04885906088748e-07
Época: 9500 Loss: 6.891851853652042e-07

Text(0, 0.5, 'Loss')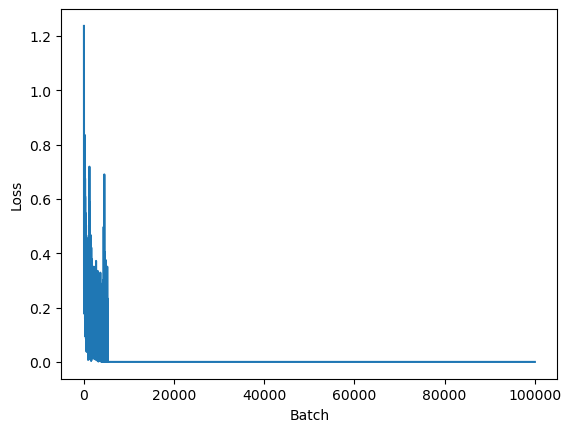

Para testar o modelo, geramos dados de teste:

# Dados de teste
NAt = 1000
NBt = 1000
Nteste = NAt + NBt

dados_teste = meias_luas(NAt, NBt, r1, r2, r3)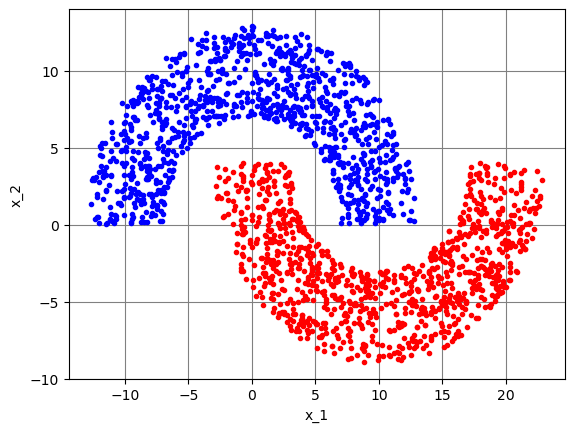

Convertemos os arrays do NumPy para tensores do PyTorch e enviamos os dados para a GPU, caso ela exista:

xteste = torch.tensor(dados_teste[:,[0,1]], dtype=torch.float32).to(device=device)
dteste = torch.tensor(dados_teste[:,[2]], dtype=torch.float32).to(device=device)

Calculamos a saída do modelo considerando os dados de teste como entrada e convertemos a saída para um array do NumPy:

yteste = model(xteste)
yteste_np = yteste.cpu().detach().numpy()

Note que, para obter o array do NumPy, é necessário:

• Chamar o método .cpu() para trazer de volta os dados da GPU, caso ela exista;
• Chamar o método .detach() para tirar o tensor do grafo computacional. Isso é necessário para que não sejam calculados os gradientes referentes às operações que eventualmente sejam feitas com yteste. Na prática, quase sempre que seja necessário converter um tensor PyTorch para um array NumPy, será necessário chamar o método .detach() antes;
• Chamar o método .numpy() para converter os dados para um array do NumPy.

Também é possível plotar a fronteira de separação, de forma semelhante à utilizada anteriormente. A diferença é a necessidade da conversão dos dados para tensores do PyTorch para utilizar o modelo e a conversão de volta para arrays do NumPy para plotar o gráfico com o Matplotlib:

# Gera a curva de separação das duas regiões
# Dados da curva de separação
Nsep = 100
x1S = np.linspace(-15, 25, Nsep).reshape(-1, 1)
x2S = np.linspace(-10, 15, Nsep).reshape(-1, 1)

# Gera pontos da grade
xx1S, xx2S = np.meshgrid(x1S, x2S)
xx1S = xx1S.reshape(-1, 1)
xx2S = xx2S.reshape(-1, 1)

# Gera array x
Ngrid = len(xx1S)
xgrid_np = np.hstack((xx1S, xx2S))

# Calcula saída para cada ponto da grade
xgrid = torch.tensor(xgrid_np, dtype=torch.float32).to(device=device)
ygrid = model(xgrid)
ygrid_dec = torch.sign(ygrid)

ygrid_np = ygrid.cpu().detach().numpy()
ygrid_dec_np = ygrid_dec.cpu().detach().numpy()

xteste_np = xteste.cpu().detach().numpy()
dteste_np = dteste.cpu().detach().numpy()

# Plota os pontos principais
fig, ax2 = plt.subplots()
for i in range(Nteste):
    if dteste_np[i] == 1:
        ax2.plot(xteste_np[i, 0], xteste_np[i, 1], ".b")
    else:
        ax2.plot(xteste_np[i, 0], xteste_np[i, 1], ".r")

# Plota pontos da grade com saída 0 (usa transparência alpha)        
l0 = np.where(ygrid_dec_np == -1)[0]
ax2.plot(xgrid_np[l0, 0], xgrid_np[l0, 1], "r.", alpha=0.1)

# Plota pontos da grade com saída 1 (usa transparência alpha)
l1 = np.where(ygrid_dec_np == 1)[0]
ax2.plot(xgrid_np[l1, 0], xgrid_np[l1, 1], "b.", alpha=0.1)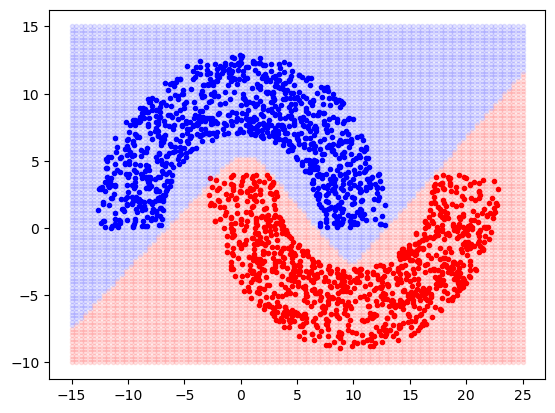

Calculando a taxa de erros:

yteste_np_dec = np.sign(yteste_np)

Taxa_de_erro = np.sum(np.absolute(dteste_np - yteste_np_dec)) * 100 / (2 * Nteste)

print(f"Taxa de erro: {Taxa_de_erro}")

Taxa de erro: 0.05

Validação cruzada hold-out

É interessante usar um conjunto de dados de validação durante o treinamento para observar se não está ocorrendo overfitting do modelo:

NAv = 50
NBv = 150
dados_val = meias_luas(NAv, NBv, r1, r2, r3)

X_val = torch.tensor(dados_val[:,[0,1]], dtype=torch.float32).to(device=device)
d_val = torch.tensor(dados_val[:,[2]], dtype=torch.float32).to(device=device)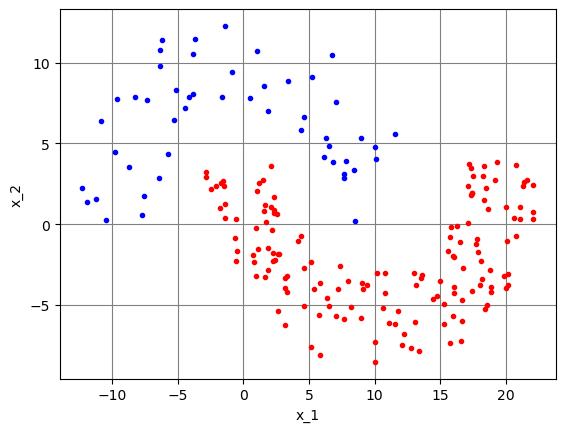

Segue um exemplo da rotina de treinamento considerando a etapa de validação. As diferenças em relação à rotina mostrado anteriormente estão destacadas. Vale notar alguns detalhes:

• A necessidade de colocar o modelo em modo treinamento (train) para atualizar os pesos e inferência (eval) para calcular o valor da função custo de validação;
• Para o cálculo da saída e do valor da função custo, não é necessário calcular gradientes.

# Reiniciando o modelo e otimizador
model = Model().to(device=device)
optimizer = torch.optim.SGD(model.parameters(), lr=eta)

# Listas para guardar o valor da função custo
# no treinamento e validação ao longo das iterações
losses = []
val_losses = []

for epoch in range(Ne):
    for n, (X, d) in enumerate(train_loader):
        X = X.to(device=device)
        d = d.to(device=device)
        
        # Necessário colocar o modelo em modo treinamento
        # na etapa de treinamento
        model.train()
        model.zero_grad()
        y = model(X)
        loss = loss_function(y, d)
        loss.backward()
        optimizer.step()

        # Validação
        # Necessário colocar o modelo em modo de inferência (eval)
        # pois algumas camadas têm comportamento diferente para inferência,
        # por exemplo, o Dropout.
        model.eval()

        # Cálculo da saída e valor da função custo com os dados de validação
        # Nesse caso, não é necessário calcular gradientes, por isso é utilizado
        # o bloco with torch.no_grad():
        with torch.no_grad():
            y_val = model(X_val)
            val_loss = loss_function(y_val, d_val)

        # Armazena o valor da função custo de treinamento e validação
        losses.append(loss.item())
        val_losses.append(val_loss.item())
        
        # Mostra os valores da função custo de treinamento e validação
        # a cada 500 épocas        
        if epoch % 500 == 0 and n == dados_treino.shape[0]//Nb - 1:
            print(f"Epoch: {epoch} Loss: {loss} Val. Loss: {val_loss}")

plt.figure()
plt.plot(losses)
plt.plot(val_losses, alpha=0.8)
plt.legend(["Loss", "Val. Loss"])
plt.xlabel("Batch")
plt.ylabel("Loss")

Epoch: 0 Loss: 0.4288952946662903 Val. Loss: 0.4373363256454468
Epoch: 500 Loss: 0.1020800769329071 Val. Loss: 0.1234327182173729
Epoch: 1000 Loss: 0.18264535069465637 Val. Loss: 0.36254554986953735
Epoch: 1500 Loss: 0.18082109093666077 Val. Loss: 0.2632644772529602
Epoch: 2000 Loss: 0.2237672060728073 Val. Loss: 0.3758035898208618
Epoch: 2500 Loss: 0.1505267173051834 Val. Loss: 0.07806681096553802
Epoch: 3000 Loss: 0.10975215584039688 Val. Loss: 0.06523850560188293
Epoch: 3500 Loss: 0.12872742116451263 Val. Loss: 0.07306171208620071
Epoch: 4000 Loss: 0.19222404062747955 Val. Loss: 0.08486053347587585
Epoch: 4500 Loss: 0.07514382153749466 Val. Loss: 0.07600489258766174
Epoch: 5000 Loss: 0.10347875207662582 Val. Loss: 0.06272117793560028
Epoch: 5500 Loss: 0.07646853476762772 Val. Loss: 0.06404448300600052
Epoch: 6000 Loss: 0.07575170695781708 Val. Loss: 0.06895849108695984
Epoch: 6500 Loss: 0.09453247487545013 Val. Loss: 0.06083502247929573
Epoch: 7000 Loss: 0.08741973340511322 Val. Loss: 0.07605186849832535
Epoch: 7500 Loss: 0.22517231106758118 Val. Loss: 0.05372380092740059
Epoch: 8000 Loss: 0.12835191190242767 Val. Loss: 0.05745967850089073
Epoch: 8500 Loss: 0.11189435422420502 Val. Loss: 0.0843060091137886
Epoch: 9000 Loss: 0.08424719423055649 Val. Loss: 0.12814004719257355
Epoch: 9500 Loss: 0.07224565744400024 Val. Loss: 0.12872619926929474

Text(0, 0.5, 'Loss')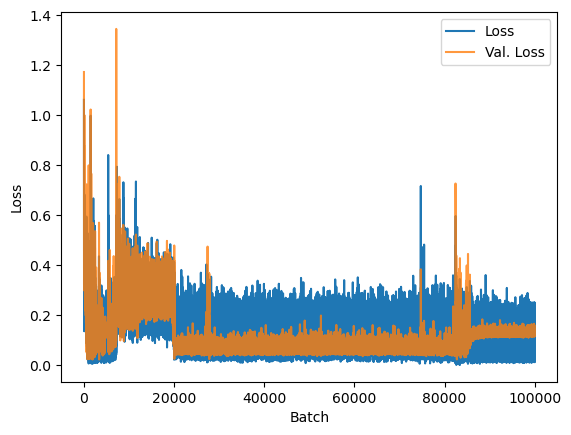

Nesse caso, note que o valor da função custo utilizando o conjunto de validação aumenta por volta da iteração 80000, o que indica overfitting.

Utilizando outras funções de ativação

O PyTorch disponibiliza uma lista grande de funções de ativação que podem ser utilizadas. Para referência, acesse https://pytorch.org/docs/stable/nn.html#non-linear-activations-weighted-sum-nonlinearity.

Para usar ReLU, por exemplo, utiliza-se a função nn.ReLU:

class Model(nn.Module):
    def __init__(self):
        super().__init__()        
        self.model = nn.Sequential(
            nn.Linear(2, 3),
            nn.ReLU(),
            nn.Linear(3, 5),
            nn.ReLU(),
            nn.Linear(5, 2),
            nn.ReLU(),
            nn.Linear(2, 1),
            nn.Tanh(),
        )

    def forward(self, x):
        output = self.model(x)
        return output

Outra função muito usada é a sigmoide, nos casos em que é necessário limitar uma saída entre 0 e 1. A implementação é feita com nn.Sigmoid():

class Model(nn.Module):
    def __init__(self):
        super().__init__()        
        self.model = nn.Sequential(
            nn.Linear(2, 3),
            nn.Sigmoid(),
            nn.Linear(3, 5),
            nn.Sigmoid(),
            nn.Linear(5, 2),
            nn.Sigmoid(),
            nn.Linear(2, 1),
            nn.Sigmoid(),
        )

    def forward(self, x):
        output = self.model(x)
        return output

Utilizando dropout

Para utilizar Dropout, basta adicionar camadas do tipo nn.Dropout(n), em que n representa a proporção de neurônios que deve ser desativada. No exemplo a seguir é utilizado Dropout de 10% para os neurônios da primeira camada:

class Model(nn.Module):
    def __init__(self):
        super().__init__()        
        self.model = nn.Sequential(
            nn.Linear(2, 3),
            nn.Tanh(),
            nn.Dropout(0.1),
            nn.Linear(3, 5),
            nn.Tanh(),
            nn.Linear(5, 2),
            nn.Tanh(),
            nn.Linear(2, 1),
            nn.Tanh(),
        )

    def forward(self, x):
        output = self.model(x)
        return output

Utilizando o otimizador Adam

Para utilizar o Adam, basta criar o otimizador usando torch.optim.Adam:

optimizer = torch.optim.Adam(model.parameters(), lr=eta, betas=(0.9, 0.999))

Utilizando a função custo da entropia cruzada

A função custo da entropia cruzada binária é implementada pela classe torch.nn.BCELoss. Para utilizá-la, basta definir:

loss_function = nn.BCELoss()

No caso de classificação multiclasse, pode-se utilizar a classe torch.nn.CrossEntropyLoss. Vale notar que essa função custo espera comparar um vetor de \(C\) posições com um número de \(0\) a \(C-1\).

Inicialização de pesos

Uma forma de inicializar os pesos da rede é definir uma função para inicializar os parâmetros de um elemento do modelo e usar o método .apply() para aplicar essa função à todos os elementos do modelo:

class Model(nn.Module):
    def __init__(self):
        super().__init__()        
        self.model = nn.Sequential(
            nn.Linear(2, 3),
            nn.Tanh(),
            nn.Linear(3, 5),
            nn.Tanh(),
            nn.Linear(5, 2),
            nn.Tanh(),
            nn.Linear(2, 1),
            nn.Tanh(),
        )

    def forward(self, x):
        output = self.model(x)
        return output

device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")    

model = Model().to(device=device)    
    
def weights_init(m):
    classname = m.__class__.__name__
    if classname.find('Linear') != -1:
        torch.nn.init.xavier_normal_(m.weight)
        torch.nn.init.zeros_(m.bias)

model.apply(weights_init)

Model(
  (model): Sequential(
    (0): Linear(in_features=2, out_features=3, bias=True)
    (1): Tanh()
    (2): Linear(in_features=3, out_features=5, bias=True)
    (3): Tanh()
    (4): Linear(in_features=5, out_features=2, bias=True)
    (5): Tanh()
    (6): Linear(in_features=2, out_features=1, bias=True)
    (7): Tanh()
  )
)

Nesse exemplo, é usada a inicialização de Xavier, com distribuição Gaussiana (torch.nn.init.xavier_normal_). Além dela, há diversas outras alternativas, listadas em https://pytorch.org/docs/stable/nn.init.html.