Análise de Componentes Principais
\[ \newcommand{\AM}{{\mathbf A}} \newcommand{\IM}{{\mathbf I}} \newcommand{\vM}{{\mathbf v}} \newcommand{\xM}{{\mathbf x}} \newcommand{\yM}{{\mathbf y}} \newcommand{\E}{{\rm E}} \]
A redução do número de variáveis de entrada de um modelo preditivo é chamada de redução de dimensionalidade. Menos variáveis de entrada podem resultar em um modelo mais simples que, por sua vez, pode ter melhor desempenho ao fazer previsões de dados novos.
A técnica mais popular para redução de dimensionalidade em Aprendizado de Máquina é a Análise de Componentes Principais (Principal Component Analysis - PCA). Essa técnica de Álgebra Linear reduz a dimensionalidade de um conjunto de dados no qual há um grande número de dados correlacionados, mantendo o máximo possível da variação presente no conjunto. Essa redução é alcançada pela transformação para um novo conjunto de variáveis não correlacionadas e que são ordenadas de modo que as primeiras retenham a maior parte da variação das originais.
A seguir vamos detalhar essa técnica.
Maximizando a variância
Considere um conjunto de dados \(\{\mathbf{x}_n\}\), em que \(n=1, 2, \ldots, N\) e \(\mathbf{x}_n \in \mathbb{R}^{D}\), ou seja, os vetores coluna \(\mathbf{x}_n\) têm dimensão \(D\times 1\) e elementos reais. O objetivo do PCA é projetar os dados em um espaço de dimensão \(M<D\) e ao mesmo tempo maximizar a variância dos dados projetados. Neste momento, vamos assumir que \(M\) é conhecido. Há técnicas para determinar um valor apropriado para \(M\), como veremos posteriormente.
Considere a projeção em um espaço de uma dimensão \(M=1\). Podemos definir a direção deste espaço, usando um vetor coluna de dimensão \(D\times 1\), denotado por \(\mathbf{u}_1\). Por conveniência e sem perda de generalidade, vamos assumir que \(\mathbf{u}_1^{\rm T}\mathbf{u}_1=\|\mathbf{u}_1\|^2=1\), já que estamos interessados na direção do vetor \(\mathbf{u}_1\) e não em sua magnitude. Cada vetor \(\mathbf{x}_n\) do conjunto de dados é então projetado no escalar \(p_{1n}=\mathbf{u}_1^{\rm T}\mathbf{x}_n\). A média dos dados projetados vale
\[ \overline{p}_1=\frac{1}{N}\sum_{n=1}^{N}p_{1n}=\frac{1}{N}\sum_{n=1}^{N}\mathbf{u}_1^{\rm T}\mathbf{x}_n=\mathbf{u}_1^{\rm T}\left[\frac{1}{N}\sum_{n=1}^{N}\mathbf{x}_n\right]=\mathbf{u}_1^{\rm T}\overline{\mathbf{x}} \]
em que \(\overline{\mathbf{x}}\) é o valor médio do conjunto de dados. A variância dos dados projetados é dada por
\[ \sigma_{p_1}^2=\frac{1}{N}\sum_{n=1}^{N}(p_{1n}-\overline{p})^2=\frac{1}{N}\sum_{n=1}^{N}(\mathbf{u}_1^{\rm T}\mathbf{x}_n-\mathbf{u}_1^{\rm T}\overline{\mathbf{x}})^2 \] \[ =\frac{1}{N}\sum_{n=1}^{N}(\mathbf{u}_1^{\rm T}\mathbf{x}_n\mathbf{x}_n^{\rm T}\mathbf{u}_1 + \mathbf{u}_1^{\rm T}\overline{\mathbf{x}}\,\overline{\mathbf{x}}^{\rm T}\mathbf{u}_1) - \frac{2}{N} \sum_{n=1}^{N}\mathbf{u}_1^{\rm T}\mathbf{x}_n\overline{\mathbf{x}}^{\rm T}\mathbf{u}_1. \]
Note que o segundo somatório do lado direito da última igualdade dessa expressão vale \[ \frac{2}{N} \sum_{n=1}^{N}\mathbf{u}_1^{\rm T}\mathbf{x}_n\overline{\mathbf{x}}^{\rm T}\mathbf{u}_1= 2 \mathbf{u}_1^{\rm T}\left[\frac{1}{N}\sum_{n=1}^{N}\mathbf{x}_n\right]\overline{\mathbf{x}}^{\rm T}\mathbf{u}_1= 2 \mathbf{u}_1^{\rm T}\overline{\mathbf{x}}\,\overline{\mathbf{x}}^{\rm T}\mathbf{u}_1. \]
Assim, podemos escrever a variância \(\sigma_{p_1}^2\) como \[ \sigma_{p_1}^2=\frac{1}{N}\sum_{n=1}^{N}(\mathbf{u}_1^{\rm T}\mathbf{x}_n\mathbf{x}_n^{\rm T}\mathbf{u}_1 - \mathbf{u}_1^{\rm T}\overline{\mathbf{x}}\,\overline{\mathbf{x}}^{\rm T}\mathbf{u}_1)= \mathbf{u}_1^{\rm T} \left[\frac{1}{N}\sum_{n=1}^{N}(\mathbf{x}_n\mathbf{x}_n^{\rm T}-\overline{\mathbf{x}}\,\overline{\mathbf{x}}^{\rm T}) \right]\mathbf{u}_1. \]
Definindo a matriz de covariância dos dados \[ \mathbf{S}=\frac{1}{N}\sum_{n=1}^{N}(\mathbf{x}_n-\overline{\mathbf{x}})(\mathbf{x}_n-\overline{\mathbf{x}})^{\rm T}, \]
e identificando que ela é termo entre colchetes da expressão anterior, chega-se finalmente a
\[ \sigma_{p_1}^2=\mathbf{u}_1^{\rm T} \mathbf{S}\mathbf{u}_1. \]
Vamos agora maximizar a variância \(\sigma_{p_1}^2\) com relação à \(\mathbf{u}_1\). Note que se trata de um critério com restrição, pois \(\|\mathbf{u}_1\|\rightarrow \infty\) maximiza \(\sigma_p^2\), mas deve ser evitado. Com esse propósito, vamos considerar a seguinte restrição \(\mathbf{u}_1^{\rm T}\mathbf{u}_1=\|\mathbf{u}_1\|^2=1\), o que leva ao critério \[ \max_{\mathbf{u}_1} \mathbf{u}_1^{\rm T} \mathbf{S}\mathbf{u}_1\;\;\text{sujeito a}\;\;\mathbf{u}_1^{\rm T}\mathbf{u}_1=1. \]
Para maximizar a variância levando em conta a restrição, pode-se considerar um multiplicador de Lagrange, denotado por \(\lambda_1\), o que leva à maximização do seguinte critério sem restrição \[ J(\mathbf{u}_1)=\mathbf{u}_1^{\rm T} \mathbf{S}\mathbf{u}_1+\lambda_1(1-\mathbf{u}_1^{\rm T}\mathbf{u}_1). \]
Calculando a derivando de \(J(\mathbf{u}_1)\) em relação à \(\mathbf{u}_1\), obtém-se \[ \frac{d J(\mathbf{u}_1)}{d\mathbf{u}_1}=\mathbf{S}\mathbf{u}_1-\lambda_1\mathbf{u_1}. \]
Igualando essa derivada a zero, chega-se a
\[\begin{equation*} \fbox{$\displaystyle \mathbf{S}\mathbf{u}_1=\lambda_1\mathbf{u}_1. $} \end{equation*}\]
Essa igualdade ocorre apenas quando \(\mathbf{u}_1\) for o autovetor de \(\mathbf{S}\) associado ao autovalor \(\lambda_1\). Para recordar isso, no Apêndice~A há uma recordação da teoria de Álgebra Linear relacionada a autovalores e autovetores.
Multiplicando ambos os lados da relação anterior à esquerda por \(\mathbf{u}_1^{\rm T}\) e usando o fato de que \(\mathbf{u}_1^{\rm T}\mathbf{u}_1=1\), obtemos \[ \sigma_{p_1}^2=\mathbf{u}_1^{\rm T}\mathbf{S}\mathbf{u}_1=\lambda_1. \]
Então a variância \(\sigma_p^2\) será máxima quando \(\mathbf{u}_1\) for o autovetor de \(\mathbf{S}\) relacionado ao maior autovalor \(\lambda_1\). Esse autovetor é conhecido como o primeiro componente principal.
Podemos adicionar componentes principais, escolhendo cada nova direção como aquela que maximiza a variância projetada entre todas as direções ortogonais possíveis às já consideradas. Dessa forma, é possível demonstrar por indução que ao considerar um espaço de dimensão \(M\), a projeção linear ótima para a qual a variância dos dados projetados é maximizada é definida pelos \(M\) autovetores \(\mathbf{u}_1, \mathbf{u}_2, \ldots, \mathbf{u}_M\) da matriz de covariância dos dados \(\mathbf{S}\), correspondentes aos seus \(M\) maiores autovalores \(\lambda_1, \lambda_2, \ldots, \lambda_M\).
Resumindo, a análise de componentes principais envolve o cálculo da média \(\overline{\mathbf{x}}\) e da matriz de covariância \(\mathbf{S}\) do conjunto de dados. Em seguida, deve-se encontrar os \(M\) autovetores de \(\mathbf{S}\) relacionados aos seus \(M\) maiores autovalores. Se levarmos em conta todos os \(D\) autovetores de \(\mathbf{S}\), não haverá redução de dimensionalidade. Trata-se de uma transformação linear ortogonal que transforma os dados para um novo sistema de coordenadas de modo que a maior variância por qualquer projeção dos dados fica ao longo da primeira coordenada (primeiro componente principal), a segunda maior variância fica ao longo da segunda coordenada (segundo componente principal) e assim por diante. O primeiro componente principal é o mais importante porque explica a maior parcela da variância dos dados, o segundo componente é o segundo mais importante e assim sucessivamente. O objetivo é descrever a maxima variabilidade do conjunto de dados original com um conjunto menor de variáveis.
Gerando um conjunto de dados não correlacionados
Vimos que os \(M\) autovetores \(\mathbf{u}_k=[u_{k1}\;u_{k2}\;\cdots\;u_{kD}]^{\rm T}\), associados aos \(M\) maiores autovalores \(\lambda_k\), \(k=1, 2, \cdots, M\) da matriz de covariância dos dados \(\mathbf{S}\) são os componentes principais. Os dados projetados em cada um desses componentes são dados por \[ p_{kn}=\mathbf{u}_k^{\rm T}\mathbf{x}_n=u_{k1}x_{1n}+u_{k2}x_{2n}+\cdots u_{kD}x_{Dn} \]
para \(k=1, 2, \cdots, M\) e \(n=1, 2 \cdots N\). Assim, os dados projetados são combinações lineares de todas as variáveis presentes nos vetores do conjunto de dados e os elementos dos autovetores, chamados de loadings na literatura, são os pesos dessas combinações.
Organizando o conjunto original de dados na matriz \[ \mathbf{X}=[\mathbf{x}_1\;\mathbf{x}_2\;\cdots\;\mathbf{x}_N] \]
e os componentes principais na matriz \[ \mathbf{U}=\left[\begin{array}{c} \mathbf{u}_1^{\rm T} \\ \mathbf{u}_2^{\rm T} \\ \vdots \\ \mathbf{u}_M^{\rm T} \end{array} \right], \]
obtemos a matriz dos dados transformados
\[ \mathbf{P}=[\mathbf{p}_1\;\mathbf{p}_2\;\cdots\;\mathbf{p}_N] \]
por meio da transformação linear \[ \mathbf{P}=\mathbf{U}\mathbf{X}, \]
ou seja, \[ \left[\begin{array}{cccc} p_{11} &p_{12} & \cdots & p_{1N} \\ p_{21} &p_{22} & \cdots & p_{2N} \\ \vdots & \vdots & \ddots & \vdots \\ p_{M1} &p_{M2} & \cdots & p_{MN} \end{array}\right]_{M\times N}=\left[\begin{array}{cccc} u_{11} &u_{12} & \cdots & u_{1D} \\ u_{21} &u_{22} & \cdots & u_{2D} \\ \vdots & \vdots & \ddots & \vdots \\ u_{M1} &u_{M2} & \cdots & u_{MD} \end{array} \right]_{M\times D}\left[\begin{array}{cccc} x_{11} &x_{12} & \cdots & x_{1N} \\ x_{21} &x_{22} & \cdots & x_{2N} \\ \vdots & \vdots & \ddots & \vdots \\ x_{D1} &x_{D2} & \cdots & x_{DN} \end{array} \right]_{D\times N}. \]
Devido à restrição do critério considerado para maximizar a variância dos dados projetados, os componentes principais, autovetores da matriz de covariância dos dados, possuem norma unitária. Além disso, de Álgebra Linear sabe-se que esses vetores são ortogonais entre si. Da teoria de Probabilidades, sabe-se que duas variáveis aleatórias são não correlacionadas quando sua covariância é nula.
Considere os dados projetados por dois componentes principais distintos, ou seja, \(\mathbf{u}_k\) e \(\mathbf{u}_{\ell}\) com \(k\neq \ell\) e \(\{k, \ell\} \in \{1, 2, \ldots, M\}\). A covariância entre esses dados é calculada como \[ {\rm cov}(k,\ell)={\rm E}\{(\mathbf{u}_k^{\rm T}\mathbf{x}_n-\mathbf{u}_k^{\rm T}\overline{\mathbf{x}})(\mathbf{x}_n^{\rm T}\mathbf{u}_\ell-\overline{\mathbf{x}}^{\rm T}\mathbf{u}_\ell)\} \]
em que \(\E\{\cdot\}\) representa a esperança matemática. Os vetores \(\mathbf{u}_k\) e \(\mathbf{u}_{\ell}\) não são variáveis aleatórias e podem sair da esperança. Assim, \[ {\rm cov}(k,\ell)=\mathbf{u}_k^{\rm T}\,\E\{\mathbf{x}_n\mathbf{x}_n^{\rm T}-\mathbf{x}_n\overline{\mathbf{x}}^{\rm T}-\overline{\mathbf{x}}\mathbf{x}_n^{\rm T}+\overline{\mathbf{x}}\,\overline{\mathbf{x}}^{\rm T}\}\,\mathbf{u}_\ell. \]
A esperança que aparece nessa expressão é a matriz de covariância dos dados, o que leva a \[ {\rm cov}(k,\ell)=\mathbf{u}_k^{\rm T}\,\mathbf{S}\,\mathbf{u}_\ell. \]
Lembrando que \(\mathbf{S}\,\mathbf{u}_\ell=\lambda_\ell\) e que \(\mathbf{u}_k^{\rm T}\mathbf{u}_\ell=0\) (os autovetores são ortogonais), chega-se
\[ {\rm cov}(k,\ell)=\lambda_\ell\mathbf{u}_k^{\rm T}\mathbf{u}_\ell=0, \]
o que mostra que os dados transformados por componentes principais distintos são não correlacionados.
Quantos componentes principais usar?
Vimos que os autovalores \(\lambda_1, \lambda_2, \ldots, \lambda_D\) da matriz de covariância dos dados \(\mathbf{S}\) são as variâncias dos dados transformados. Assim, a soma de todos os autovalores é a variância total explicada, ou seja, \[ \sigma^2_{\text{total}}=\sum_{k=1}^{D}\lambda_k. \]
Consequentemente, a proporção da variância explicada (em %) por cada componente principal \(\ell\), \(\ell=1, 2, \cdots M\) é dada por \[ \%{\rm var}_\ell=100\displaystyle\frac{\lambda_\ell}{\displaystyle\sum_{k=1}^{D}\lambda_k}=100\displaystyle\frac{\lambda_\ell}{\displaystyle\sigma^2_{\text{total}}}. \]
Como o PCA é um método usado para redução de dimensionalidade, deve-se considerar apenas os componentes que explicam a maior parte da variação dos dados. Não existe um ponto de corte absoluto para descartamos os componentes principais menos significativos. Em geral, considera-se o número de componentes principais para que a soma da proporção da variância explicada seja em torno de 80%.
Normalizando o conjunto de dados
Em geral, os elementos dos vetores de dados \(\mathbf{x}_n\) podem representar variáveis com diferentes ordens de grandeza. Diante disso, é importante normalizar os dados antes de calcular o PCA. Suponha que cada vetor \(\mathbf{x}_n\) do banco de dados seja dado por
\[ \mathbf{x}_n=[x_{1n}\;x_{2n}\;\cdots\; x_{Dn}]^{\rm T}, \]
em que cada variável \(x_{nk}\), \(k=1, 2, \ldots, D\) representa uma grandeza. A normalização mais comum dos dados leva em conta a média
\[ \overline{x}_k=\frac{1}{N}\sum_{n=1}^{N}x_{kn}, \]
e o desvio padrão de cada variável \[ \sigma_{x_k}=\sqrt{\frac{1}{N}\sum_{n=1}^{N}(x_{kn}-\overline{x}_k)^2}, \]
para \(k=1, 2, \ldots, D\). Assim, as variáveis são normalizadas como
\[ \widetilde{x}_{kn}=\frac{x_{kn}-\overline{x}_k}{\sigma_{x_k}} \]
e os vetores de dados normalizados sobre os quais o PCA deve ser calculado é dado por
\[ \widetilde{\mathbf{x}}_n=[\widetilde{x}_{1n}\;\widetilde{x}_{2n}\;\cdots\; \widetilde{x}_{Dn}]^{\rm T} \]
para \(n=1, 2, \ldots, N\).
Nas seções anteriores, a formulação do PCA foi feita sobre o conjunto de dados não normalizados \(\{\mathbf{x}_n\}\). No entanto, a normalização é aconselhável como forma de evitar enviesar a influência de certas variáveis quando as variáveis originais têm dispersões ou escalas significativamente diferentes. Quando as medidas originais já possuem dispersões semelhantes, a padronização tem pouco efeito.
Exemplos
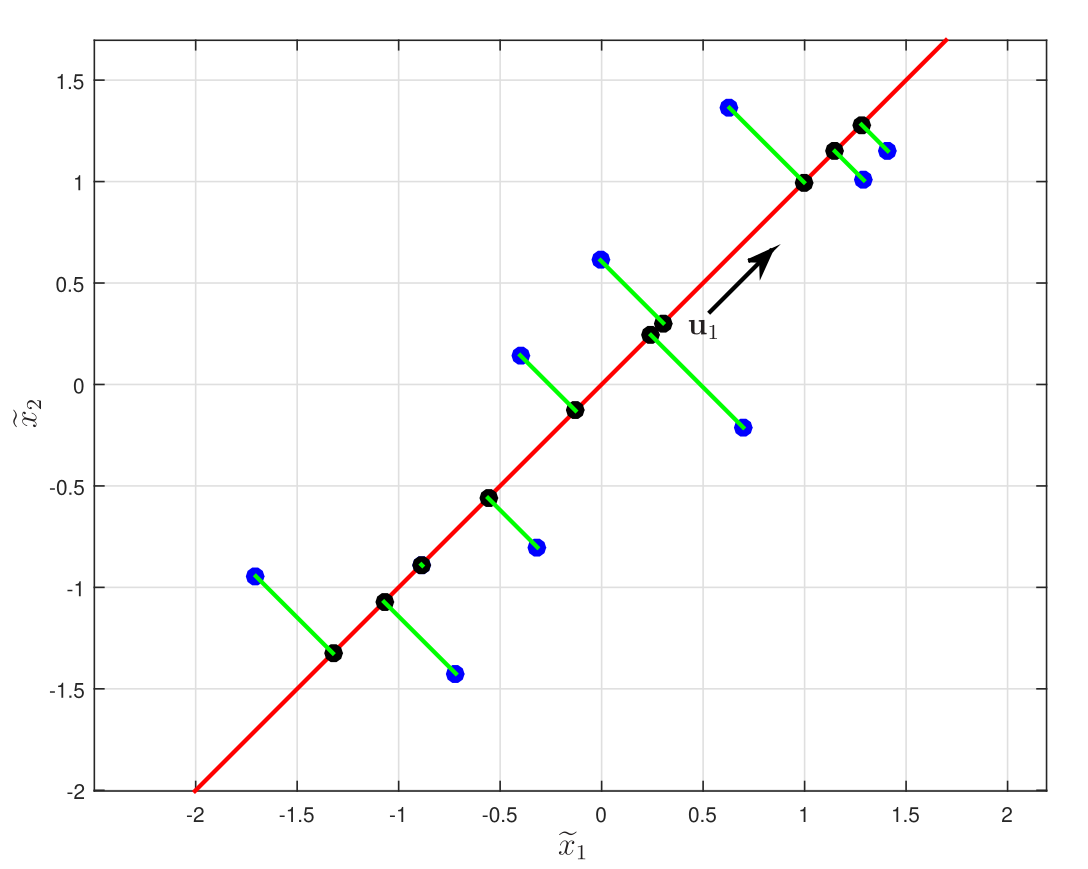
Considere que os pontos azuis indicados na Figura 1 pertencem a um conjunto de dados normalizados \(\{\widetilde{\mathbf{x}}_n\}\) com \(N=10\) e \(D=2\). Vamos considerar o subespaço gerado pelo primeiro componente principal, diminuindo a dimensão para \(M=1\). A matriz de covariância dos dados é dada por \[ \mathbf{S}=\left[\begin{array}{cc} 0,900 & 0,725 \\ 0,725 & 0,900 \end{array} \right] \]
cujos autovalores são \(\lambda_1=1,625\) e \(\lambda_2=0,1750\) e os autovetores de norma unitária associados são \(\mathbf{u}_1=[1/\sqrt{2}\;\;\;\; 1/\sqrt{2}]^{\rm T}\) e \(\mathbf{u}_2=[-1/\sqrt{2}\;\;\;\; 1/\sqrt{2}]^{\rm T}\), respectivamente. Considerando o componente principal \(\mathbf{u}_1\), autovetor associado ao maior autovalor, os dados projetados são calculados como
\[ p_n=\frac{1}{\sqrt{2}}\widetilde{x}_{1n}+\frac{1}{\sqrt{2}}\widetilde{x}_{2n}. \]
Esse componente explica \(\%{\rm var}_1=100(1,625)/(1,625+0.1750)=90,28\%\) da variância total. O PCA busca um espaço de dimensão \(M=1\), denotado pela linha vermelha tal que a projeção ortogonal dos dados originais (pontos azuis) neste subespaço maximiza a variância dos pontos projetados (pontos pretos). Uma formulação alternativa do PCA é baseada na minimização dos erros de projeção, indicados pelas linhas verdes.
O PCA pode ser usado para compressão de imagens. Para ilustrar isso, na Figura 2(a), consideramos imagem média (\(\overline{\mathbf{x}}\)) e os quatro primeiros componentes principais (\(\mathbf{u}_1,\cdots,\mathbf{u}_4\)) com os seus autovalores correspondentes baseados em imagens do dígito três da base de dados MNIST. Na Figura 2(b), são mostradas a imagem original e as imagens reconstruídas considerando 1, 10, 50 e 250 componentes principais. A medida que se aumenta o valor de \(M\), a reconstrução se torna mais precisa e é perfeita para \(M=D=784\).

Leitura adicional
O livro (Jolliffe 2002) é uma referência recomendada para quem quiser se aprofundar no assunto.
Autovalores e Autovetores
Seja \(\AM\) uma matriz \(M\times M\) com elementos constantes. Essa matriz, quando aplicada a um vetor \(\xM\) com dimensão \(M\times 1\), resulta em um vetor \(\yM\) com dimensão \(M\times 1\), ou seja,
\[\begin{equation}\label{eq:TL} \yM=\AM\, \xM. \end{equation}\]
Nota-se que a matriz \(\AM\) representa uma transformação linear que transforma um vetor \(\xM\) no vetor \(\yM\). O vetor \(\yM\) pode ser interpretado como resultado da projeção do vetor \(\xM\) nas colunas da matriz \(\AM\). De modo geral, essa transformação muda o módulo e a direção do vetor \(\xM\).
Um caso particular de grande interesse prático é aquele em que \(\xM\) é um vetor não nulo e \(\AM\,\xM\) é um múltiplo escalar de \(\xM\). Para destacar esse vetor \(\xM\) dos demais vamos denotá-lo como \(\vM\), assim,
\[ \begin{equation*} \fbox{$\displaystyle \AM\, \vM=\lambda\vM $} \end{equation*} \tag{1}\]
em que \(\lambda\) é uma constante real ou complexa. Nesse caso, a transformação linear aplicada em \(\vM\) resulta em um múltiplo escalar dele mesmo. O vetor particular \(\xM=\vM\) representa uma direção privilegiada no espaço formado pelas colunas da matriz \(\AM\), tal que a ação da transformação \(\AM\) sobre o vetor \(\vM\) age apenas sobre o módulo desse vetor mantendo a sua direção. O escalar \(\lambda\) é chamado de autovalor de \(\AM\) e \(\vM\) de autovetor associado a \(\lambda\). Cabe observar que para um dado autovalor \(\lambda\) podem existir vários vetores não nulos \(\vM\) que satisfazem a Equação 1, como veremos a seguir. Além disso, o autovetor \(\vM\) não pode ser nulo, porém, o autovalor \(\lambda\) pode ser nulo.
A obtenção dos autovalores e autovetores
Por conveniência vamos reescrever a Equação 1 da seguinte forma,
\[ \begin{equation} % \AM\, \xM-\lambda\IM\xM= \left( \AM-\lambda\IM\right)\vM=\mathbf{0}, \end{equation} \tag{2}\]
em que \(\IM\) denota a matriz identidade de dimensão \(M\times M\) e \(**0**\) um vetor de zeros de dimensão \(M\times 1\). Nota-se que \(\lambda\) é um autovalor da matriz \(\AM\) se e somente se a Equação 2 possui uma solução não trivial.
A partir da Equação 2, usando conceitos de solução de sistemas de equações e particularizando para o caso de interesse, seguem as afirmações:
A Equação 2 terá uma solução não trivial se e somente se \(\left( \AM-\lambda\IM\right)\) for singular, ou seja, \[ \begin{equation*} \fbox{$\displaystyle \det\left( \AM-\lambda\IM\right)=0. $} \end{equation*} \tag{3}\]
Ao aplicar a operação de determinante em \(\left( \AM-\lambda\IM\right)\) obtemos um polinômio em \(\lambda\), que representamos como \[ \begin{equation}\label{eq:sol2} p(\lambda)= \det\left( \AM-\lambda\IM\right)=\lambda^M+c_1\lambda^{M-1}+c_2\lambda^{M-2}\cdots c_M. \end{equation} \tag{4}\]
O polinômio \(p(\lambda)\) é chamado de polinômio característico e \(p(\lambda)=0\) é chamada de equação característica.
Nota-se que grau de \(p(\lambda)\) é \(M\), portanto, { \(p(\lambda)=0\)} possui \(M\) soluções. Essas soluções podem ser distintas, repetidas, reais ou complexas. Os valores de \(\lambda\) que satisfazem a Equação 4 são os autovalores da matriz \(\AM\). Portanto, \(\AM\) possui \(M\) autovalores que podem ser distintos, repetidos, reais ou complexos.
O conjunto de todas as soluções da Equação 2, aqui denotada como \(\cal{N}\left( \AM-\lambda\IM\right)\) é o espaço nulo de \(\AM-\lambda\IM\) e todos os autovetores da matriz \(\AM\) estão nesse espaço nulo. Assim, se \(\lambda\) é um autovalor de \(\AM\), então, \({\cal{N}}\left( \AM-\lambda\IM\right)\neq \{ 0 \}\) e qualquer subespaço não nulo em \(\cal{N}\left( \AM-\lambda\IM\right)\) é um autovetor associado a \(\lambda\). O subespaço \(\cal{N}\left( \AM-\lambda\IM\right)\) é chamado de autoespaço de \(\lambda\).
Exemplos com \(M=2\)
Nos exemplos a seguir, os autovalores são calculados a partir da Equação 3 e os autovetores associados são calculados resolvendo os sistemas de equações \(\AM\, \vM_1=\lambda_1\vM_1\) e \(\AM\, \vM_2=\lambda_2\vM_2\).
Seja a matriz \[ \AM=\left[ \begin{array}{cc} 0 & 0 \\ 0 & 1 \\ \end{array} \right] \] os autovalores e os autovetores associados são \(\lambda_1=0\) e \(\lambda_2=1\), e \[ \begin{array}{ccc} \vM_1=\left[ \begin{array}{c} 1 \\ 0 \\ \end{array} \right] & \text{ e} & \vM_2= \left[ \begin{array}{c} 0 \\ 1 \\ \end{array} \right]\text{,} \end{array} \] respectivamente. Esse exemplo ilustra o fato de que, embora o autovetor não possa ser um vetor nulo, o autovalor pode assumir o valor nulo.
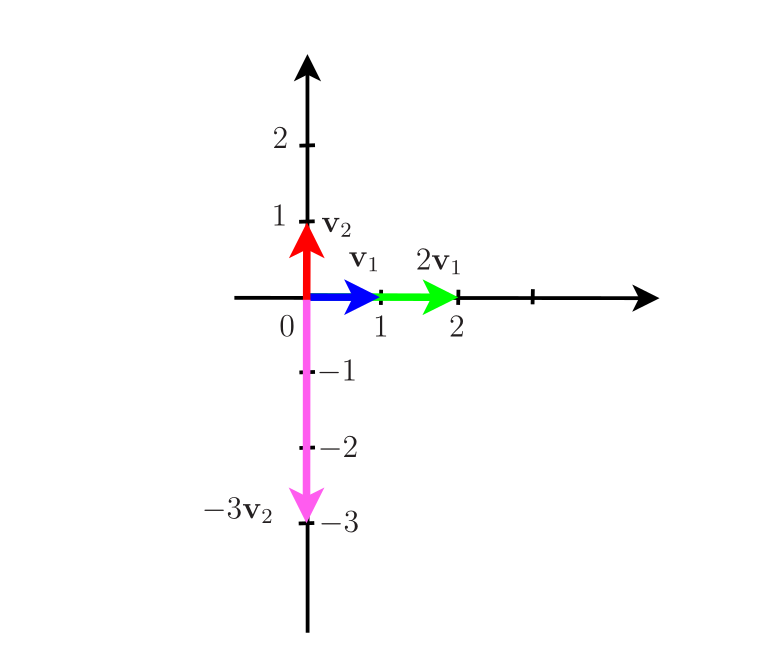
Seja a matriz \[ \AM=\left[ \begin{array}{cr} 2 & 0 \\ 0 & -3 \\ \end{array} \right] \] O polinômio característico de \(\AM\) é $ p()=(2-)(-3-)$. Portanto, os autovalores de \(\AM\) são \(\lambda_1=2\) e \(\lambda_2=-3\). Resolvendo os sistemas de equações \(\AM\, \vM_1=2\vM_1\) e \(\AM\, \vM_2=-3\vM_2\) obtemos os autovetores \(\vM_1=[ 1\,\,0]^T\) e \(\vM_2=[ 0\,\,1]^T\), respectivamente. Na Figura 3, são mostrados os vetores \(\vM_1\) e \(\vM_2\) e as suas projeções no espaço formado pelas colunas da matriz \(\AM\). Como \(\AM\) é uma matriz diagonal, os autovetores coincidem com as coordenadas do espaço Euclidiano.
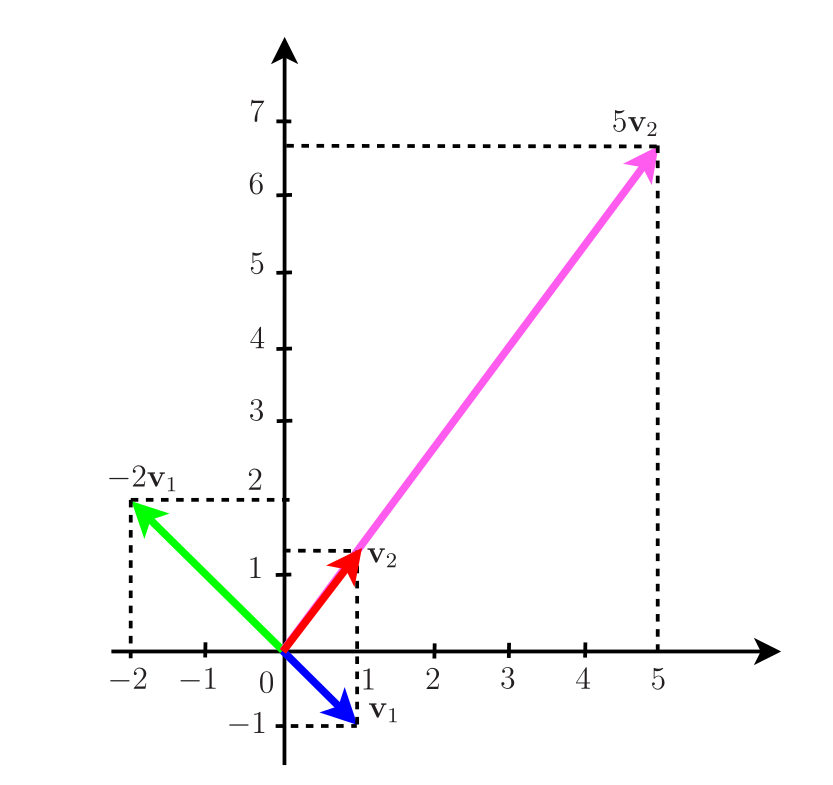
Seja a matriz \[ \AM=\left[ \begin{array}{cr} 1 & 3 \\ 4 & 2 \\ \end{array} \right]. \] O polinômio característico de \(\AM\) é \(p(\lambda)=\lambda^2-3\lambda-10=(\lambda-5)(\lambda+2)\) e consequentemente os seus autovalores são \(\lambda_1=-2\) e \(\lambda_2=5\). Resolvendo os sistemas de equações \(\AM\, \vM_1=-2\vM_1\) e \(\AM\, \vM_2=5\vM_2\) obtemos os autovetores \(\vM_1=[ 1\,\,-1]^T\) e \(\vM_2=[ 1\,\,4/3]^T\), respectivamente.
Na Figura 4, são mostrados os vetores \(\vM_1\) e \(\vM_2\) e as suas projeções no espaço formado pelas colunas da matriz \(\AM\). Nesse caso, como \(\AM\) não é uma matriz diagonal, os autovetores não coincidem com as coordenadas do espaço Euclidiano.
De modo geral, nota-se que cada autovalor de \(\AM\) possui uma infinidade de autovetores associados. Assim, são também autovetores de \(\AM\) os vetores \(\bar\vM_1=\vM_1/||\vM_1||=[ 1\,\,-1]^T/\sqrt{2}\) e \(\bar\vM_2=\vM_2/||\vM_2||=[ 3\,\,4]^T/5\).
Os autovetores \(\bar\vM_1\) e \(\bar\vM_2\) são particularmente interessantes porque possuem norma unitária.
- No MatLab faça \(help\,\, eig\). Use esse comando para conferir os autovalores e autovetores dos Exemplos \(1\), \(2\) e \(3\). Os autovetores fornecidos pelo MatLab possuem sempre norma unitária.